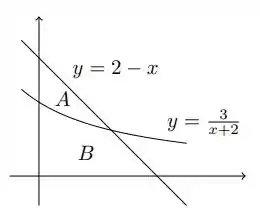
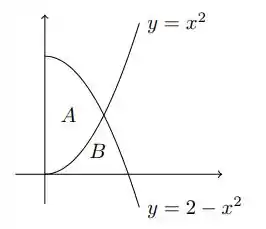Listas de Cálculo 2 - Profº M. C. Fenille de Cálculo 2 da UFU - Primeira Lista de Exercícios

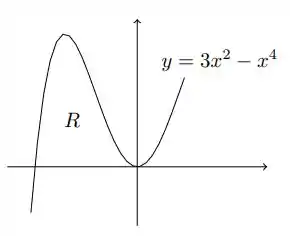
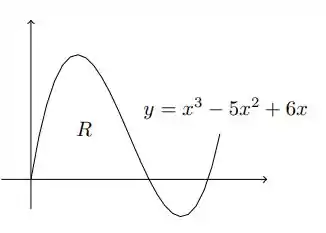
O gráfico da função é dado na figura ao lado. Calcule as integrais a seguir, interpretando-as em termos de áreas:

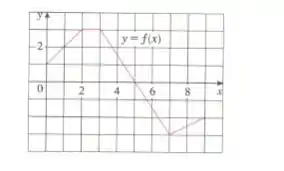
Calcule cada integral definida a seguir, interpretando- a em termos de áreas:

a)

Calcule cada integral definida a seguir, interpretando- a em termos de áreas:

b)

Calcule cada integral definida a seguir, interpretando- a em termos de áreas:

c)

Calcule cada integral definida a seguir, interpretando- a em termos de áreas:

d)

Dado que e , determine .

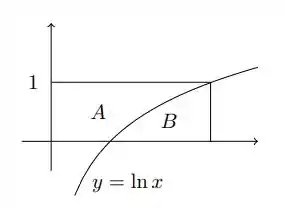
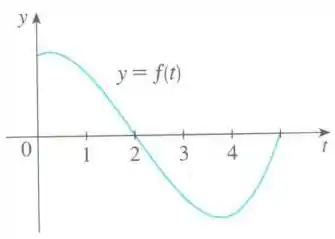
Seja , em que é a função cujo gráfico é mostrado na figura. Dentre os valores , decida qual é o maior e qual é o menor.

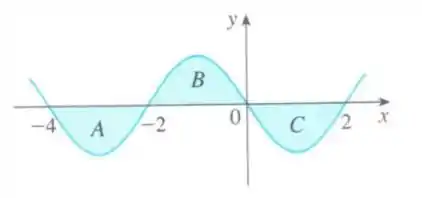
A figura abaixo mostra o gráfico de uma função e destaca três regiões: e , todas com área igual a . Determine as seguintes integrais:

Calcule a derivada sendo dadas:

Calcule a derivada sendo dadas:

Calcule a derivada sendo dadas:

Calcule a derivada sendo dadas:

Calcule a derivada sendo dadas:

Calcule a derivada sendo dadas:

Dada , determine o intervalo em que é crescente.

Sendo e , encontre .

Sendo , contínua e , determine .

Encontre uma função e um número real tal que para todo .

Calcule as seguintes integrais definidas:

a)

Calcule as seguintes integrais definidas:

b)

Calcule as seguintes integrais definidas:

c)

Calcule as seguintes integrais definidas:

d)

Calcule as seguintes integrais definidas:

e)

Calcule as seguintes integrais indefinidas:

f)

Calcule as seguintes integrais indefinidas:

g)

Calcule as seguintes integrais indefinidas:

h)

Sendo que é contínua e , determine e .

Esboce e calcule a área da região do plano- determinada pelas inequações:

a)

e

Esboce e calcule a área da região do plano- determinada pelas inequações:

b)

e

Esboce e calcule a área da região do plano- determinada pelas inequações:

c)

e

Esboce e calcule a área da região do plano- determinada pelas inequações:

d)

e

Esboce e calcule a área da região do plano- determinada pelas inequações:

e)

e

Esboce e calcule a área da região do plano- determinada pelas inequações:

f)

e

Esboce e calcule a área da região do plano- determinada pelas inequações:

g)

e

Esboce e calcule a área da região do plano- determinada pelas inequações:

h)

e

Esboce a região delimitada pelas curvas e determine sua área:

a)

Esboce a região delimitada pelas curvas e determine sua área:

b)

Esboce a região delimitada pelas curvas e determine sua área:

c)

Determine a área da região indicada em cada figura.

a)

Determine a área da região indicada em cada figura.

b)

Determine a área da região indicada em cada figura.

c)

Determine as áreas das regiões e indicadas em cada figura:

a)

Determine as áreas das regiões e indicadas em cada figura:

b)

Determine as áreas das regiões e indicadas em cada figura:

c)

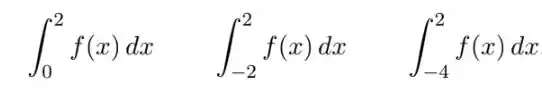
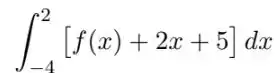
Esboce e calcule o volume do sólido descrito.

a) Uma calota de altura , de uma esfera de raio .

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

a)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

b)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

c)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

d)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

e)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

f)

Determine se cada integral imprópria é convergente ou divergente. Calcule as convergentes.

g)

Faça o mesmo que no exercício anterior.

a)

Faça o mesmo que no exercício anterior.

b)

Faça o mesmo que no exercício anterior.

c)

Utilize o critério da comparação para decidir se cada integral converge ou diverge.

a)

Utilize o critério da comparação para decidir se cada integral converge ou diverge.

b)

Utilize o critério da comparação para decidir se cada integral converge ou diverge.

c)

Esboce e calcule o volume do sólido descrito.

b) Uma pirâmide de altura e base retangular de lados e .

Esboce e calcule o volume do sólido descrito.

c) O sólido cuja base é o semicírculo , cujas secções perpendiculares ao eixo são triângulos equiláteros.

Esboce e calcule o volume do sólido descrito.

d) O sólido cuja base é a região elíptica e cujas secções perpendiculares ao eixo são semicírculos.

Esboce e calcule o volume do sólido descrito.

e) O sólido cuja base é a região delimitada pela parábola e pelo eixo , e cujas secções perpendiculares ao eixo são quadrados.