UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 17d
Esboce e calcule o volume do sólido descrito.
d) O sólido cuja base é a região elíptica e cujas secções perpendiculares ao eixo são semicírculos.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar e calcular o volume do sólido cuja base é a região elíptica e cujas secções perpendiculares ao eixo são semicírculos.
Ou seja, queremos encontrar o volume do seguinte sólido:
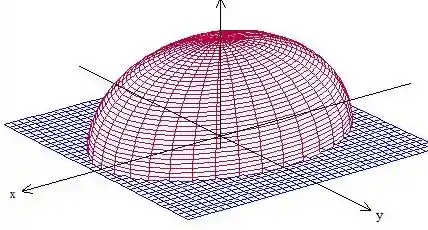
Para isso, vamos considerar como a altura do sólido no eixo .
Não entendeu? Então bora junto 😉
Passo 2
Bom... uma forma de calcularmos o volume desse sólido é considerarmos que ele trata-se da metade de um elipsoide (figura abaixo), o que é descrito pela seguinte forma:
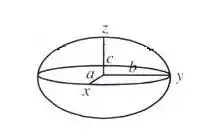
E sua equação é dada por:
Pela equação dada na questão , e considerando a altura do elipsoide, temos que:
Passo 3
Dessa forma, o volume do sólido que queremos encontrar é a metade do volume do elipsoide, ou seja:
Onde
Logo, substituindo, temos:
Passo 4
Dessa forma, substituindo e , temos:
Entendeu direitinho? Responde aee ;)
