Esboce e calcule a área da região do plano- determinada pelas inequações:
b)
e
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcularmos a área da região determinada pelas seguintes inequações:
e
Em outras palavras, queremos descobrir a seguinte integral (veja o gráfico do Passo 2):
Não entendeu? Então bora junto 😉
Passo 2
Bom... plotando o gráfico, temos:
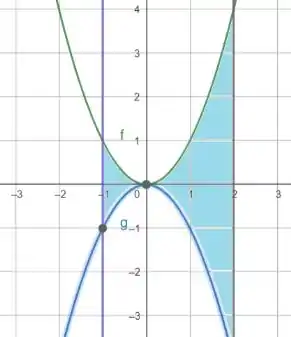
Passo 3
Bom... dessa forma, resolvendo a integral, temos:
Entendeu direitinho? Responde aee ;)
