UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 17e
Esboce e calcule o volume do sólido descrito.
e) O sólido cuja base é a região delimitada pela parábola e pelo eixo , e cujas secções perpendiculares ao eixo são quadrados.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar e calcular o volume do sólido cuja base é a região delimitada pela parábola e pelo eixo , e cujas secções perpendiculares ao eixo são quadrados. Ou seja:
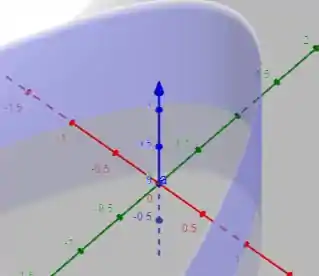
Onde o consideramos:
- Eixo : vermelho;
- Eixo : verde;
- Eixo : azul.
Também, devemos considerar apenas a parte positiva do eixo para o sólido a ser estudado.
Para calcular o seu volume, podemos descobrir a área da base (que é uma parábola) e multiplicar por sua altura em , que denominaremos de .
Não entendeu? Então bora junto 😉
Passo 2
Bom... Calculando a área da parábola descrita por , podemos integrar da seguinte forma:
Passo 3
Dessa forma, o volume é dado pela multiplicação da área pela altura :
Entendeu direitinho? Responde aee ;)
