UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 16a
Determine as áreas das regiões e indicadas em cada figura:
a)
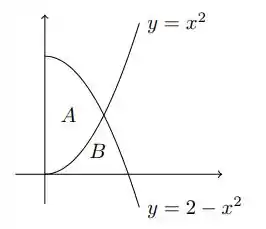
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinar a área das regiões e sabendo que estas pertencem às funções e , como mostra a figura.
Perceba que a área é dada pela diferença de por .
E, por outro lado, a área é dada pela soma de por .
Dessa forma, basta integrarmos a diferença entre duas funções para descobrir a área desejada!!
Não entendeu? Então bora junto 😉
Passo 2
Bom... para a área , temos:
Passo 3
Já para a área , temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x