UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille - Primeira Lista de Exercícios, Questão 3
Dado que e , determine .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para resolver a seguinte integral:
Dado que e .
Bom... como não sabemos a função, então não podemos aplicar as técnicas de integração.
Assim, podemos utilizar o princípio de que a integral é a área “debaixo” de uma curva!!
Não entendeu? Então bora junto 😉
Passo 2
Bom... seja o gráfico para uma qualquer:
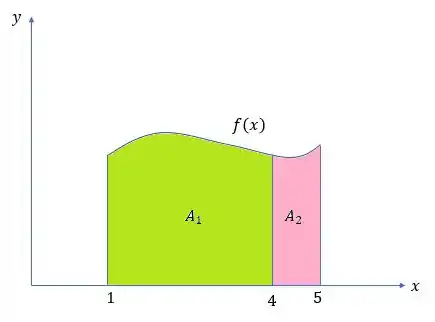
Passo 3
Assim, sendo , para e , temos então que:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 θ 6 sec 2 θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x