Calcule cada integral definida a seguir, interpretando- a em termos de áreas:
c)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para resolver a seguinte integral:
E também pede para respondermos em termos de área.
Sabemos que a integral pode ser interpretada como a área debaixo de uma determinada curva.
Assim, basta analisarmos a função contida na integral e verificar a área naquele intervalo!!
Não entendeu? Então bora junto 😉
Passo 2
Bom... dessa forma, plotando o gráfico e analisando o intervalo de a :
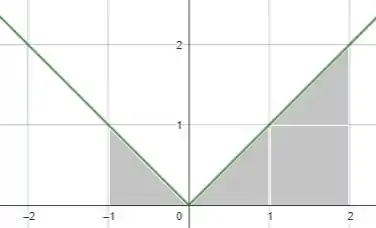
Passo 3
Assim, temos que a área é dada por:
Entendeu direitinho? Responde aee ;)
