UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 17a
Esboce e calcule o volume do sólido descrito.
a) Uma calota de altura , de uma esfera de raio .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar e calcular o volume de uma calota de altura em uma esfera de raio , ou seja:
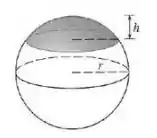
Podemos calcular o volume da seguinte forma:
Não entendeu? Então bora junto 😉
Passo 2
Bom... dessa forma, pela figura temos que:
E
Sabemos também que:
Assim, temos que:
Passo 3
Agora, aplicando na integral e resolvendo, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .