UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille - Primeira Lista de Exercícios, Questão 4
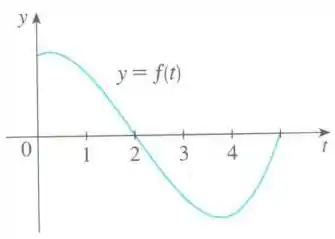
Seja , em que é a função cujo gráfico é mostrado na figura. Dentre os valores , decida qual é o maior e qual é o menor.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um gráfico de uma função qualquer e nos dá alguns valores .
A questão nos pede para dizer qual é o maior valor e qual é o menor.
Passo 2
Bom... pelo gráfico, sabe-se que e que , pois nesse intervalo a função é positiva.
Além disso, , pois a partir de o valor da integral é reduzido.
Para mais, , pois a parte negativa da função é maior em área que a parte positiva.
Passo 3
Assim, juntando essas informações, verifica-se que é a maior e é a menor.
Entendeu direitinho? Responde aee ;)
Resposta
é a maior e é a menor.
Exercícios de Livros Relacionados
Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 θ 6 sec 2 θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x