UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 17c
Esboce e calcule o volume do sólido descrito.
c) O sólido cuja base é o semicírculo , cujas secções perpendiculares ao eixo são triângulos equiláteros.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar e calcular o volume do sólido cuja base é o semicírculo , cujas secções perpendiculares ao eixo são triângulos equiláteros.
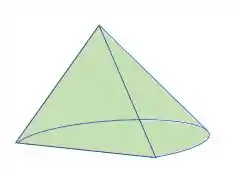
Para isso, vamos ter que estudar o triangulo equilátero e buscar uma relação com o semicírculo para podermos encontrar o volume.
Não entendeu? Então bora junto 😉
Passo 2
Bom... vamos colocar a área do triângulo equilátero em função de .
Para isso, devemos saber que a área do triângulo equilátero de lado é dada por:
Assim, o lado do triângulo em relação ao lado da abcissa da circunferência é dada por:
Logo, substituindo na equação da área, temos:
Passo 3
Dessa forma, o volume é dado pela integral da área no intervalo do semicírculo de raio :
Entendeu direitinho? Responde aee ;)
