UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 17b
Esboce e calcule o volume do sólido descrito.
b) Uma pirâmide de altura e base retangular de lados e .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar e calcular o volume de uma pirâmide de altura e base retangular de lados e , ou seja, queremos descobrir da seguinte figura:
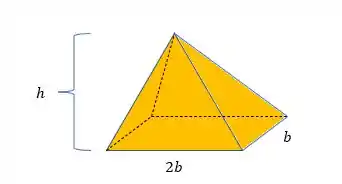
Para isso, podemos pegar a vista de uma das laterais e fazer uma semelhança de triângulos para podermos seguir calculando o volume na integral.
Não entendeu? Então bora junto 😉
Passo 2
Bom... Para um corte transversal de altura , temos:
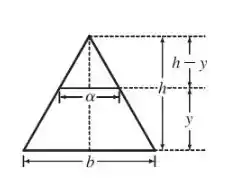
Por semelhança de triângulo, temos:
E similarmente para o outro corte transversal, temos:
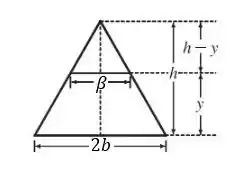
Por semelhança de triângulos, de forma análoga, temos:
Passo 3
Dessa forma, o volume é dado pela integral da área em relação a altura da pirâmide , veja:
Entendeu direitinho? Responde aee ;)
