UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille - Primeira Lista de Exercícios, Questão 5
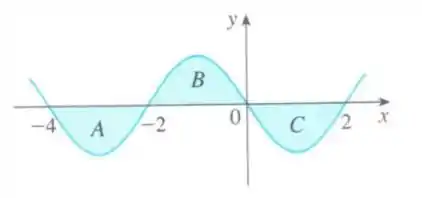
A figura abaixo mostra o gráfico de uma função e destaca três regiões: e , todas com área igual a . Determine as seguintes integrais:
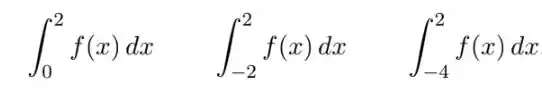
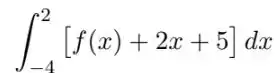
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um gráfico de uma função qualquer e nos pede para resolver algumas integrais baseada nas áreas da figura.
Podemos fazer isso analisando os limites das integrais!!
E aí? Bora lá??
Passo 2
Bom... na primeira integral, temos:
Pelo gráfico, vemos que trata-se do intervalo , veja:
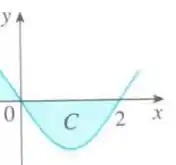
Dessa forma, como se situa-se no lado negativo, temos então que:
Passo 3
Na segunda integral, temos:
Pelo gráfico, vemos que trata-se da soma dos intervalos e , veja:
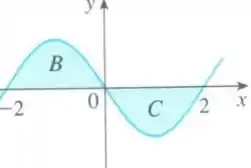
Dessa forma, temos então que:
Passo 4
Na segunda integral, temos:
Pelo gráfico, vemos que trata-se da soma dos intervalos e , veja:
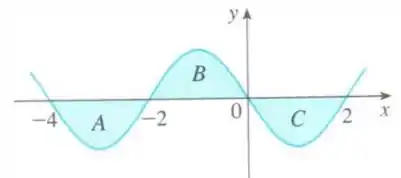
Dessa forma, temos então que:
Passo 5
Na segunda integral, temos:
Pelo gráfico, vemos que trata-se da soma dos intervalos e , veja:
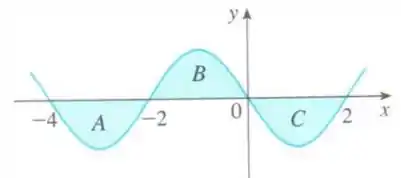
Dessa forma, temos então que:
Entendeu direitinho? Responde aee ;)
