UFU – Cálculo 2 – Lista 1 – Questão 1
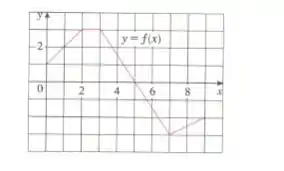
O gráfico da função é dado na figura ao lado. Calcule as integrais a seguir, interpretando-as em termos de áreas:
Passo 1
Oi pessoal, tudo bem? Vamos começar?
O problema começa nos dando o gráfico da função aqui:
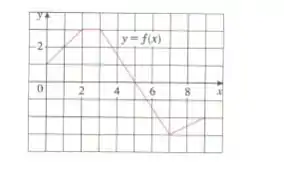
E pediu para calcular as integrais
Mas relaxa, vou fazer passo a passo com você!
Passo 2
A primeira integral é essa aqui
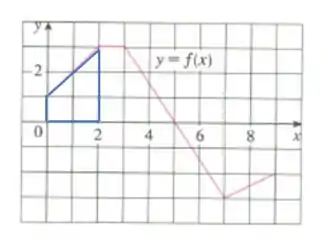
É um trapézio de base maior , menor e altura :
Beleza?
Agora nossa missão é resolver as outras de forma bem similar!
Passo 3
Nossa integral é essa aqui
Mas sabemos quanto vale de até , então vamos separar em três:
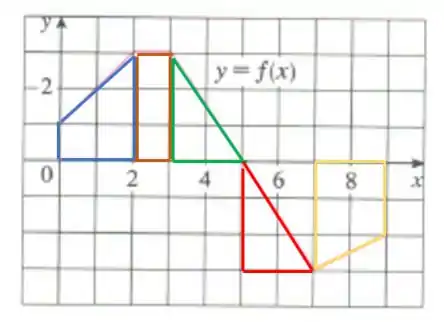
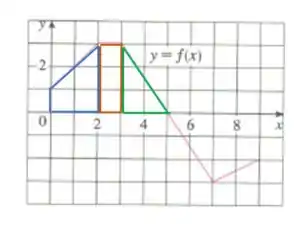Graficamente é:
A área azul vale (do passo anterior), a área laranja é um retângulo e a verde um triângulo! Agora é só calcular e somar tudo
Passo 4
Nossa próxima integral é
Note que no gráfico ela está abaixo do eixo , então o valor da área deve ser negativo.
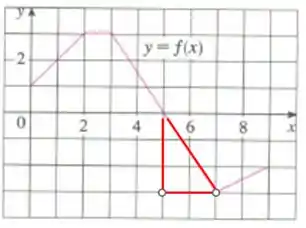
(uma área propriamente dita não é negativa, mas estamos calculando a área de uma função que pode, por exemplo, representar o trabalho realizado e esse sim, pode ser negativo)
E por fim
Temos quase todos os intervalos calculados, só faltou de até :
Que é um trapézio novamente! E essa área será negativa também, pois está abaixo do eixo !
Beleza? Espero ter ajudado!
Até a próxima!