UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 14b
Esboce a região delimitada pelas curvas e determine sua área:
b)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar a área delimitadas pelas três equações dadas e, com isso, calcular a área.
Para isso, primeiro vamos esboçar a figura:
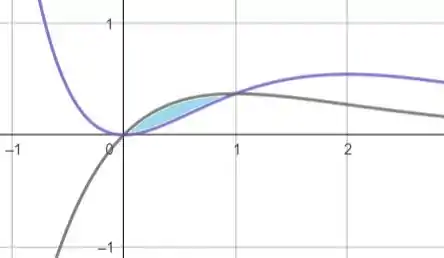
Agora, analisando o gráfico, para calcular a área em azul devemos aplicar a seguinte integral:
Não entendeu? Então bora junto 😉
Passo 2
Bom... dessa forma, resolvendo a integral, temos:
Onde:
E, resolvendo por partes, encontramos:
Passo 3
Nesse sentido, substituindo em , temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x