Considere o produto .
(I) Se é injetiva, então é injetiva.
(II) Se , então
(a) Ambas as afirmações são falsas.
(b) Ambas as afirmações são verdadeiras.
(c) (I) é falsa e (II) é verdadeira.
(d) (I) é verdadeira e (II) é falsa.
Passo 1
Vamos começar lembrando que uma matriz representa uma transformação linear.
E uma transformação é apenas um outro nome pra função.
Então, assim como nas funções, as transformações também possuem domínio, contradomínio e imagem.
Vamos começar definindo que as transformações A e B sejam tais que:
(Já já vamos falar da C :D)
Assim como as funções, também podemos compor transformações lineares.
Se aplicamos primeiro a transformação B e depois a A, a composta vai ser dada por:
Que é a matriz C!
Então a transformação C é dada por:
Agora vamos ver as alternativas.
Passo 2
Passo 3
(I) Se é injetiva, então é injetiva.
Uma transformação é injetiva quando elementos diferentes do domínio possuem imagens diferentes.
Vamos olhar o diagrama abaixo:
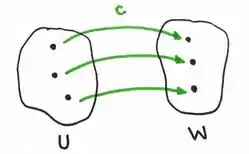
Ele mostra uma transformação C que é injetiva, pelo motivo que acabei de falar.
Mas lembra que vimos que C é a composta de A com B?
Então, podemos expandir esse diagrama desse jeito:
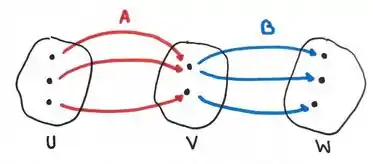
Nesse caso, a transformação A não é injetiva, pois temos elementos distintos com a mesma imagem.
Então a afirmação (I) é falsa: C ser injetiva não faz com que A seja injetiva.
Passo 4
(II) Se , então
Foi dado pra gente que
Mas agora temos que , então:
Agora vamos lembrar duas coisas:
- A imagem de B é o espaço gerado pelas colunas
- O núcleo de A é formado pelos elementos que são solução do sistema homogêneo
Como o espaço gerado pelas colunas de B faz com que A resulte em uma matriz nula, então a imagem de B está contida no domínio de A.
Essa afirmação é verdadeira.
Resposta
(c) (I) é falsa e (II) é verdadeira.