Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Injetividade, Sobrejetividade e Bijetividade de uma TL

Ver Teoria
Exercício 381234567891011121314151617181920212223242526272829303132333435363739

Enunciado

UFRJ; Provas Antigas; Álgebra Linear; P2 2022.1; Questão 3

A transformação linear abaixo que é sobrejetiva é:

  1. A projeção ortogonal sobre o plano 8 x - 4 y - 5 z = 0 em R 3
  2. A projeção ortogonal sobre a reta L { ( - 4,1 ) } do R 2
  3. Um cisalhamento em R 2
  4. A projeção sobre a reta L { ( - 6,2 ) } do R 2 , seguida de uma reflexão sobre o eixo x em R 2

Passo 1

Fala galera, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é simples. Queremos saber qual transformação é Sobrejetiva. Lembram o que é uma transformação sobrejetiva?

Uma transformação é sobrejetiva se a dimensão da imagem da transformação é igual a dimensão do contra domínio.

Então vamos verificar qual das alternativas satisfaz a definição.

Passo 2

Começando pela letra a), temos:

A projeção ortogonal sobre o plano 8 x - 4 y - 5 z = 0 em R 3

E aí, vamos analisar essa transformação? Então, estamos pegando todos os pontos do R 3 e projetando eles em um plano. Logo a nossa imagem é o próprio plano. Um plano tem dimensão 2, mas o plano está em R 3 que tem dimensão 3. Então essa transformação NÃO é sobrejetiva.

Pelo mesmo argumento, vamos ter que a transformação da alternativa b) que é:

A projeção ortogonal sobre a reta L { ( - 4,1 ) } do R 2

é falsa.

Passo 3

Vamos checar a alternativa c). A transformação é o cisalhamento em R 2 . Lembram o que é cisalhamento?

Vamos relembrar.

De forma simplificada, cisalhamento é uma transformação que pega os retângulos do R 2 e transforma eles em paralelogramas. Tome como exemplo a imagem abaixo.

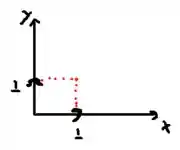
Bem, pela figura acima, podemos ver que os vetores da base do R 2 são levados em vetores LI em um cisalhamento. Ou seja, tem dimensão 2. Logo a transformação é sobrejetiva.

E com isso chegamos a conclusão que a letra c) contém uma transformação linear sobrejetiva

Prontinho, pessoal!! Finalizamos mais uma!!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

c )

Exercícios de Livros Relacionados

Seja a um vetor em R 3 fixado. Decida se a fórmula T v = a × v define um operador linear injetor de R 3 . Explique seu raciocínio.
Seja E uma matriz elementar 2 × 2 fixada. Decida se a fórmula T A = E A define um operador linear injetor de M 2 × 2 . Explique seu raciocínio.
Em cada parte, determine se a multiplicação por A é uma transformação linear injetora. A = 1 - 2 2 - 4 - 3 6 A = 1 3 5 7 2 - 1 2 4 - 1 3 0 0 A = 4 - 2 1 5 5 3
Seja a aplicação T :R 2 → R 3 x , y → ( x + k y ,x + k ,y ) Verificar em que caso(s) T é linear:a) k = x b) k = 1 c) k = 0
Consideremos a transformação linear T : R 2 → R 2 definida por T x , y = ( 3 x - 2 y ,x + 4 y ) . Utilizar os vetores u = ( 1 ,2 ) e v = ( 3 , - 1 ) para mostra que T 3 u + 4 v = 3 T u + 4 T ( v ) .