Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Injetividade, Sobrejetividade e Bijetividade de uma TL

Ver Teoria
Exercício 101234567891112131415161718192021222324252627282930313233343536373839

Enunciado

Transformações Lineares e Teorema Núcleo-Imagem

À questão “Dado v = x 0 y 0 z 0 ∈ M 3 × 1 fixo, a transformação T : M 3 × 3 ⟶ M 3 × 1 dada por T A = A v é linear?”, Andrezinho respondeu da seguinte maneira:

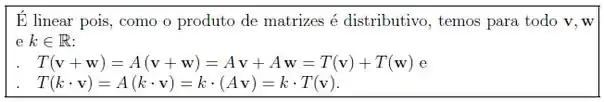
( a ) Embora T seja realmente uma transformação linear, a justificativa do Andrezinho não está correta. Qual foi o erro que ele cometeu?

( b ) Mostre que T é linear.

( c ) Existe algum v tal que T seja injetiva?

( d ) Determine uma base do núcleo e uma base da imagem de T quando v = 1 0 - 1

Passo 1

Letra ( a )

Andrezinho errou a expressão da T L e também quem são os elementos do seu domínio. Assim, ele fez variar o vetor coluna v , w enquanto seu domínio é na verdade M 3 × 3 , ou seja quem deveria variar deveria ser uma matriz A ∈ M 3 × 3 e não um vetor coluna!

Assim, ele fixou a matriz A , e tomou v , w como suas variáveis do problema, provando para uma S :   M 3 × 1 ⟶ M 3 × 1 dada por S v = A v e não uma T : M 3 × 3 ⟶ M 3 × 1 dada por T A = A v .

Passo 2

Letra ( b )

Antes de começar, NÃO É NECESSÁRIO EXPANDIR A MATRIZ A COMO UMA 3 × 3 !! BASTA USAR AS PROPRIEDADES DAS MATRIZES!

Assim para provar que é linear basta fazermos:

  • T A 1 + A 2 = T A 1 = T ( A 2 )
  • T k A = k T A

Vamos provar essa primeiro:

I   T A 1 + A 2 = T A 1 + T A 2   ( I I )

Desenvolvendo o lado ( I I ) temos que:

T A 1 + T A 2 = A 1 v + A 2 v = A 1 + A 2 v = T A 1 + A 2

E assim vemos que I = ( I I ) !

Passo 3

Agora vamos provar que

I I I   T k A = k T A   ( I V )

Assim, vamos desenvolver o lado ( I I I ) :

T k A = k A v = k A v = k T ( A )

E assim podemos ver que os lados ( I I I ) e ( I V ) são iguais, E, portanto provamos as condições para nossa T ser linear!

Passo 4

Letra ( c )

Talvez a pergunta tenha ficado um pouco confusa. Acho que fica mais claro assim: existe algum v para que T seja injetiva?

Bom, vamos ver se ela é injetiva primeiro. Pelo Teorema Núcleo-Imagem, podemos ver que:

dim ⁡ N u c T + dim ⁡ I m T = dim ⁡ M 3 × 3 ⇒

dim ⁡ N u c T + dim ⁡ I m T = 9

Se ela for injetiva, dim ⁡ N u c T = 0 , e assim, a dim ⁡ I m T = 9 . Só que sabemos que I m T ⊂ M 3 × 1 e, portanto, a dim ⁡ I m T deve ser no máximo 3 (que e é a dimensão do contradomínio). Assim, não existe nenhum v que torne isso possível.

Passo 5

Letra ( d )

Para achar uma base para o núcleo, primeiramente, devemos fazer:

T A = A v = 0

Desenvolvendo:

a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 1 0 - 1 = 0 ⇒

a 1 - a 3 = 0 ⇒ a 1 = a 3 a 4 - a 6 = 0 ⇒ a 4 = a 6 a 7 - a 9 = 0 ⇒ a 7 = a 9

Substituindo num elemento genérico do domínio temos:

a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 = a 1 a 2 a 1 a 4 a 5 a 4 a 7 a 8 a 7 =

= a 1 1 0 1 0 0 0 0 0 0 + a 2 0 1 0 0 0 0 0 0 0 + a 4 0 0 0 1 0 1 0 0 0

+ a 5 0 0 0 0 1 0 0 0 0 + a 7 0 0 0 0 0 0 1 0 1 + a 8 0 0 0 0 0 0 0 1 0

E assim uma possível base para o núcleo é:

β = 1 0 1 0 0 0 0 0 0 ,   0 1 0 0 0 0 0 0 0 ,   0 0 0 1 0 1 0 0 0 ,   0 0 0 0 1 0 0 0 0 ,   0 0 0 0 0 0 1 0 1 ,   0 0 0 0 0 0 0 1 0

Passo 6

Para a imagem, basta fazermos:

T A = A v ⇒

a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 1 0 - 1 = a 1 - a 3 a 4 - a 6 a 7 - a 9

Expandindo temos a imagem!

a 1 - a 3 a 4 - a 6 a 7 - a 9 = a 1 1 0 0 + a 3 - 1 0 0 + a 4 0 1 0 + a 6 0 - 1 0 + a 7 0 0 1 + a 9 0 0 - 1

E assim uma possível base é:

α = 1 0 0 ,   0 1 0 ,   0 0 1

Resposta

( c ) Não.

( d )

Base para o núcleo: β = 1 0 1 0 0 0 0 0 0 ,   0 1 0 0 0 0 0 0 0 ,   0 0 0 1 0 1 0 0 0 ,   0 0 0 0 1 0 0 0 0 ,   0 0 0 0 0 0 1 0 1 ,   0 0 0 0 0 0 0 1 0

Base para a imagem:

α = 1 0 0 ,   0 1 0 ,   0 0 1

Exercícios de Livros Relacionados

Seja a um vetor em R 3 fixado. Decida se a fórmula T v = a × v define um operador linear injetor de R 3 . Explique seu raciocínio.
Seja E uma matriz elementar 2 × 2 fixada. Decida se a fórmula T A = E A define um operador linear injetor de M 2 × 2 . Explique seu raciocínio.
Em cada parte, determine se a multiplicação por A é uma transformação linear injetora. A = 1 - 2 2 - 4 - 3 6 A = 1 3 5 7 2 - 1 2 4 - 1 3 0 0 A = 4 - 2 1 5 5 3
Seja a aplicação T :R 2 → R 3 x , y → ( x + k y ,x + k ,y ) Verificar em que caso(s) T é linear:a) k = x b) k = 1 c) k = 0
Consideremos a transformação linear T : R 2 → R 2 definida por T x , y = ( 3 x - 2 y ,x + 4 y ) . Utilizar os vetores u = ( 1 ,2 ) e v = ( 3 , - 1 ) para mostra que T 3 u + 4 v = 3 T u + 4 T ( v ) .