Seja uma transformação linear dada por:
(b) Determine uma base para a imagem de T. T é sobrejetora?
Passo 1
Vamos pegar um vetor genérico que pertence à imagem.
Então:
Montando a matriz aumentada desse sistema e escalonando:
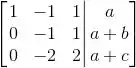
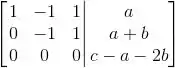
Para que esse sistema tenha solução, o lado direito da última linha também tem que ser 0:
Os vetores da imagem são então:
Como os vetores e são LI e os vetores da imagem são combinações lineares deles, então eles formam uma base para a imagem:
Passo 2
Para a transformação linear ser sobrejetiva:
Mas a dimensão da imagem é 2 (só temos 2 vetores na base), então ela não é sobrejetiva.
Resposta
(b) Base:
Não é sobrejetiva.
Exercícios de Livros Relacionados
Seja a um vetor em R 3 fixado. Decida se a fórmula T v = a × v define um operador linear injetor de R 3 . Explique seu raciocínio.
Seja E uma matriz elementar 2 × 2 fixada. Decida se a fórmula T A = E A define um operador linear injetor de M 2 × 2 . Explique seu raciocínio.
Em cada parte, determine se a multiplicação por A é uma transformação linear injetora. A = 1 - 2 2 - 4 - 3 6 A = 1 3 5 7 2 - 1 2 4 - 1 3 0 0 A = 4 - 2 1 5 5 3
Seja a aplicação T :R 2 → R 3 x , y → ( x + k y ,x + k ,y ) Verificar em que caso(s) T é linear:a) k = x b) k = 1 c) k = 0
Consideremos a transformação linear T : R 2 → R 2 definida por T x , y = ( 3 x - 2 y ,x + 4 y ) . Utilizar os vetores u = ( 1 ,2 ) e v = ( 3 , - 1 ) para mostra que T 3 u + 4 v = 3 T u + 4 T ( v ) .