Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Coulomb

Ver Teoria
Exercício 731234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727475

Enunciado

UFSC, Sem Campus, Física 3, Provas de Física 3 - Profº Abílio - 1ª Avaliação Parcial (P1), Questão 2

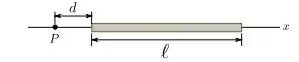
Uma barra de comprimento l está sobre o eixo x conforme mostra a Figura 2. Ela possui uma densidade de carga uniforme λ. Determine o campo elétrico no ponto P, situado a uma distância d da barra.

Passo 1

Eaew, belezinha?

Temos que determinar o campo elétrico no ponto P. Como a barra está no eixo x, temos que a direção do campo também será no eixo x. Como a barra possui densidade de carga uniforme, podemos somar as contribuições de cada elemento de carga para o campo:

d E = d q 4 π ε 0 x 2

Vamos identificar esse elemento de carga e integrar para somar todas essas contribuições.

Então vamos lá!

Passo 2

Podemos escrever o elemento de carga em termos da densidade linear da barra:

d q = λ   d x

Considerando que a posição do ponto P é na origem do eixo x, podemos integrar para d ≤ x ≤ d + l . Assim, temos a integral:

E = ∫ d d + l λ d x 4 π ε 0 x 2 = λ 4 π ε 0 ∫ d d + l d x x 2

Resolvendo essa integral simples:

E = λ 4 π ε 0 ( - 1 x ) | d d + l

E = λ 4 π ε 0 ( 1 d - 1 d + l ) .

Como a barra está no eixo x, temos que a direção do campo também será no eixo x:

  → E = λ 4 π ε 0 l d ( d + l ) i ^ .

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

  → E = λ 4 π ε 0 l d ( d + l ) i ^ .

Exercícios de Livros Relacionados

Uma carga puntiforme de 5,0μ C está localizada em x = 1,0m , y = 3,0m , e uma carga puntiforme de - 4,0μ C está localizada em x = 2,0m , y = - 2,0 . (a) Determine o módulo, a direção e o sentido do ca
Duas cargas positivas iguais, q , estão no eixo y , uma carga puntiforme está em y = + a e a outra está em y = - a . (a) Mostre que, no eixo x , a componente x do campo elétrico é dada por E x = 2 k q
Uma partícula puntiforme que tem carga de 5,00μ C está localizada em x = 0 e y = 0 e uma puntiforme que tem carga q está localizada em x = 4,00c m , y = 0 . A força elétrica em uma partícula puntiform
Uma carga puntiforme q 1 = 4,0μ C está na origem é uma carga puntiforme q 2 = 6,0μ C está no eixo x em x = 3,0m . (a) Determine o campo elétrico na carga q 2 . (b) Determine o campo elétrico na carga
Duas cargas puntiformes positivas, com carga Q , estão no eixo y , uma em y = + a e outra em y = - a . (a) Mostre que a intensidade do campo elétrico no eixo x é máxima em x = a / 2 e em x = - a / 2 ,