Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 21 – seção 4 - Problema 19.
(Cap 21 Ex – 19) Na Fig. 21-25, a partícula , de carga , e a partícula , de carga , estão a uma distância uma da outra em um eixo . Se as três partículas permanecem onde estão quando uma partícula 3 de carga é colocada nas proximidades das partículas e, determine (a) a coordenada da partícula : (b) a coordenada da partícula ; (c) a razão .
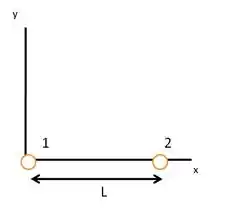
Passo 1
E ai galerinha, tudo certinho?
Bora resolver essa comigo?
- Vamos supor que a partícula é colocada numa posição qualquer, com relação à origem. Assim, a força eletrostática total a que ela está submetida é igual a
- Para que a partícula esteja em equilíbrio, então ela deve estar entre as outras duas cargas. Então,
- Agora, vamos olhar para a força resultante sobre a partícula . Essa força também é nula como conseqüência da condição de equilíbrio do sistema. Então:
Usando o fato de que e e que , encontramos:
Passo 2
Passo 3
Usando os dados do enunciado e essa expressão, a gente encontra que:
Resposta
Exercícios de Livros Relacionados
Uma carga puntiforme de 5,0μ C está localizada em x = 1,0m , y = 3,0m , e uma carga puntiforme de - 4,0μ C está localizada em x = 2,0m , y = - 2,0 . (a) Determine o módulo, a direção e o sentido do ca
Duas cargas positivas iguais, q , estão no eixo y , uma carga puntiforme está em y = + a e a outra está em y = - a . (a) Mostre que, no eixo x , a componente x do campo elétrico é dada por E x = 2 k q
Uma partícula puntiforme que tem carga de 5,00μ C está localizada em x = 0 e y = 0 e uma puntiforme que tem carga q está localizada em x = 4,00c m , y = 0 . A força elétrica em uma partícula puntiform
Uma carga puntiforme q 1 = 4,0μ C está na origem é uma carga puntiforme q 2 = 6,0μ C está no eixo x em x = 3,0m . (a) Determine o campo elétrico na carga q 2 . (b) Determine o campo elétrico na carga
Duas cargas puntiformes positivas, com carga Q , estão no eixo y , uma em y = + a e outra em y = - a . (a) Mostre que a intensidade do campo elétrico no eixo x é máxima em x = a / 2 e em x = - a / 2 ,