Três cargas são colocadas em três vértices de um quadrado de de lado, como mostrado abaixo.
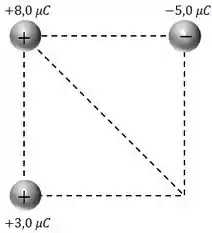
Qual é o módulo aproximado da força eletrostática resultante que uma carga de sentirá se for colocada no quarto vértice?
;
;
;
;
;
Passo 1
Bom, para começar, vamos posicionar a carga de no vértice do quadrado que está vazio e numerar as cargas que irão exercer uma força sobre ela para facilitar a resolução:
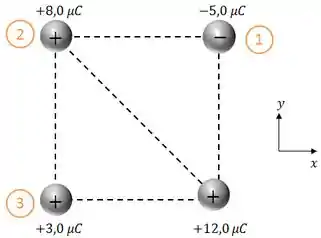
Além disso, adotamos um sistema de referência pra facilitar a análise.
Show de bola! Agora vamos calcular a força exercida por cada uma dessas cargas sobre a nossa carga de .
Passo 2
- Carga 1:
- Carga 2:
- Carga 3:
Como as cargas possuem sinais opostos, a força de interação entre elas será de atração, logo, a força terá o sentido e módulo dado por:
Onde:
Dessa forma:
E o vetor força elétrica gerada pela carga 1 será:
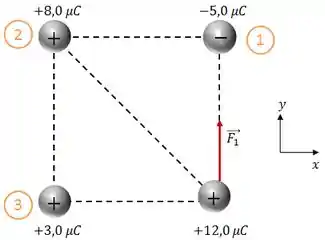
Passo 3
Agora as duas cargas possuem o mesmo sinal, assim, a força de interação entre elas será de repulsão, como ilustrado na figura abaixo:
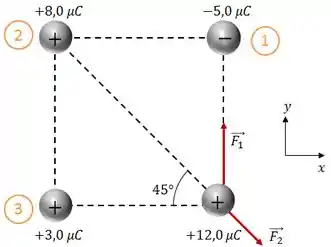
O módulo dessa força é dado por:
O que muda agora é a carga e a distância , que corresponde à diagonal do quadrado:
Dessa forma:
E o vetor força elétrica gerada pela carga 2 será:
Passo 4
Novamente, as duas cargas possuem o mesmo sinal, sendo a força entre elas de repulsão, logo, no sentido , como indicado na figura abaixo:
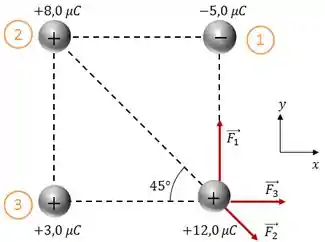
O módulo da força elétrica gerada pela carga 3 é dada por:
Onde:
Dessa forma:
E o vetor força elétrica gerada pela carga 1 será:
Passo 3
A força elétrica resultante sobre a carga de será:
Finalmente, o módulo da força resultante será:
Resposta
;