Duas esferas idênticas de massa estão suspensas em fios de seda (??) de comprimento , como indicado na figura abaixo. Cada esfera possui a mesma carga; logo, . O raio de cada esfera é muito pequeno em comparação à distância entre as esferas, de modo que elas podem ser consideradas cargas puntiformes. Mostre que, se o ângulo for pequeno, a distância no equilíbrio entre as esferas será dada por .
Sugestão: quando for pequeno, então
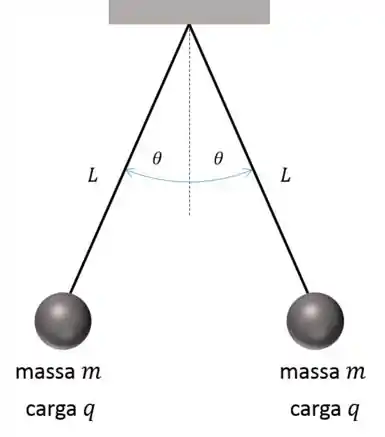
Passo 1
Belezinha. Questão que remete à Física I, a parada é fazer as equações do equilíbrio para as esferas:
Na realidade, por causa da simetria só precisa fazer as equações pra uma delas. Então partiu.
Decompondo para a esfera da esquerda:
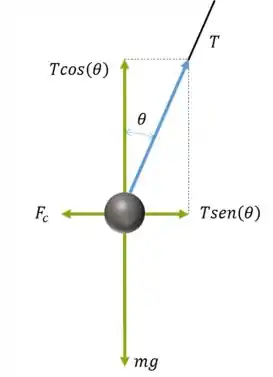
Temos que as equações são:
A brincadeira é resolver para a distância entre as esferas, que ainda não apareceu na equação. Ainda tem uma incógnita que não tratamos, que é a força repulsiva entre as esferas.
Passo 2
Sabemos também que a força entre as esferas é dada pela equação de Coulomb:
Substituindo:
Agora falta se livrar dessa tensão, que não é dado.
Passo 3
Usando a equação do equilíbrio em , temos:
Substituindo:
Arrumando a bagunça:
Agora é a hora de usar o dado do enunciado!
Passo 4
Como foi dado que, para pequeno temos:
Tiramos da figura o seno:
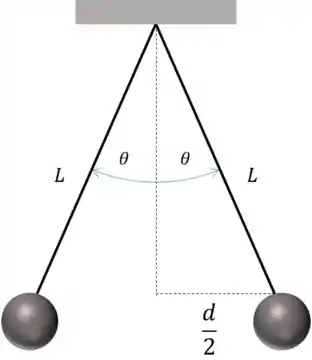
Substituindo na equação:
Agora é só isolar o :
Substituindo o valor de :
Temos que:
E fim de papo. O resto é só tirar a raiz:
Resposta
Ei, a resposta está no passo a passo :)