Duas esferas condutoras são suspensas por meio de fios isolantes idênticos e neutros de comprimento . A aceleração da gravidade local tem módulo igual a . Sabendo que as duas esferas possuem a mesma carga e a mesma massa , e que o sistema está em equilíbrio quando o ângulo entre os fios vale , podemos afirmar que satisfaz a relação:

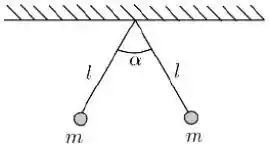
Escolha uma:

Com isso podemos equacionar essas quatro forças assim:

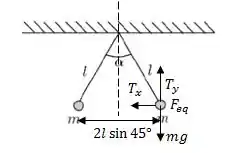
E sabendo também que a componente vertical é proporcional ao cosseno de , e que a componente horizontal vai com o seno, temos o seguinte sistema:

E podemos substituir a primeira equação na segunda:

E temos a seguinte expressão:

E agora podemos trabalhar um pouco com ela! Vamos lá?

Temos que , e que , daí temos:

E isolando temos:

Tranquilo?

E analisando as alternativas, a correta é a (d).

Espero ter ajudado!