Uma partícula está rodeada por partículas carregadas situadas em dois anéis concêntricos a ela, conforma mostrado na figura abaixo. Todas as partículas estão fixas em suas posições e suas cargas são indicadas na figura. Os raios dos anéis interno e externo valem e , respectivamente. Utilizando o sistema de coordenadas indicado, qual é a força eletrostática resultante sobre a partícula de carga ?
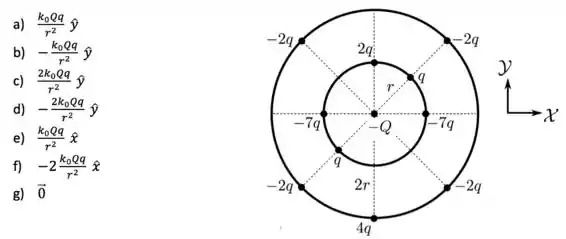
Passo 1
Esse tanto de cargas assusta e pensar que teríamos que fazer a conta de todas as forças sobre a carga já cansa a gente, não é mesmo? Na verdade, não precisamos fazer toda essa contaiada se percebemos que um monte dessas forças se cancelam aos pares \0/. Dá uma olhada na figura abaixo e na correspondência entre pares de cargas circuladas com o mesma cor.
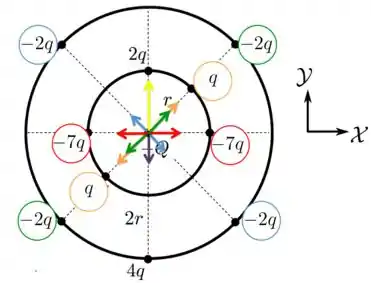
Todas os círculos com mesma cor mostram os pares de carga que dão origem a forças sobre a carga de mesma intensidade, mesma direção, porém sentido contrário e, por isso, se cancelam. As forças sobre são representadas pelos vetores situados no centro onde está .
Os únicos vetores que não se cancelam são os de cor amarela e roxa na direção do eixo que, apesar de estarem na mesma direção e terem sentidos contrários, não possuem o mesmo módulo como no caso das outras forças analisadas. Eles se referem a forças de atração devidas às cargas e que estão, respectivamente, a uma distância e de .
Portanto, basta calcular essas duas forças e partir para o abraço...\0/
Passo 2
A força em devida à carga (vetor em amarelo na figura acima) está na direção e é dada por
A força em devida à carga (vetor em roxo na figura acima) também está na direção , mas aponta para o sentido negativo do eixo e é dada por
Passo 3
A resultante das forças sobre é, portanto, a soma vetorial abaixo
SUGESTÃO: em questões com várias cargas estáticas em distribuições simétricas como as desse problema (que só precisamos calcular apenas duas forças e somá-las!!), procure sempre verificar se existem pares de cargas contribuindo com parcelas que se cancelam, pois isso pode te ajudar a ganhar tempo na solução do problema. Se liga nisso, OK? ;-).
Resposta
Portanto, a letra a) é a resposta correta.