UFRJ – Física 3 2020.2 – P2 – Questão 7
Três partículas de cargas e , e estão localizadas nos pontos de coordenadas , e , respectivamente, num sistema de eixos cartesianos. Sabendo que e são os vetores unitários nas direções e , podemos dizer que a força resultante na partícula de carga devido às outras duas partículas é dada por:
Passo 1
Fala galera, tudo bem? Vou começar fazendo um desenho das forças sobre a carga :
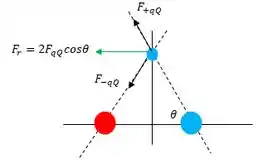
O cosseno é:
Passo 2
Assim a força é:
E a força resultante é:
E o vetor vai ser ao longo do eixo negativo:
Analisando as alternativas, a correta é a (f).
Resposta
Exercícios de Livros Relacionados
Uma carga puntiforme de 5,0μ C está localizada em x = 1,0m , y = 3,0m , e uma carga puntiforme de - 4,0μ C está localizada em x = 2,0m , y = - 2,0 . (a) Determine o módulo, a direção e o sentido do ca
Duas cargas positivas iguais, q , estão no eixo y , uma carga puntiforme está em y = + a e a outra está em y = - a . (a) Mostre que, no eixo x , a componente x do campo elétrico é dada por E x = 2 k q
Uma partícula puntiforme que tem carga de 5,00μ C está localizada em x = 0 e y = 0 e uma puntiforme que tem carga q está localizada em x = 4,00c m , y = 0 . A força elétrica em uma partícula puntiform
Uma carga puntiforme q 1 = 4,0μ C está na origem é uma carga puntiforme q 2 = 6,0μ C está no eixo x em x = 3,0m . (a) Determine o campo elétrico na carga q 2 . (b) Determine o campo elétrico na carga
Duas cargas puntiformes positivas, com carga Q , estão no eixo y , uma em y = + a e outra em y = - a . (a) Mostre que a intensidade do campo elétrico no eixo x é máxima em x = a / 2 e em x = - a / 2 ,