Duas cargas puntiformes positivas estão localizadas sobre o eixo sobre os pontos e . Uma outra carga puntiforme negativa está localizada em algum ponto sobre o eixo .
- Faça um diagrama de corpo livre mostrando as forças que atuam sobre a carga ;
- Encontre as componentes e da força resultante da ação das duas cargas positivas sobre . (Sua resposta deve envolver somente , , , e a coordenada da terceira carga.)
- Qual é a força resultante sobre a carga quando ela está na origem ()?
Passo 1
a) O que a gente tem neste exercício está mostrado na figura abaixo. Como as cargas são positivas, a carga negativa , que está na posição sobre o eixo , sente uma força de aproximação na direção da linha que une e as cargas positivas , como desenho para você abaixo.
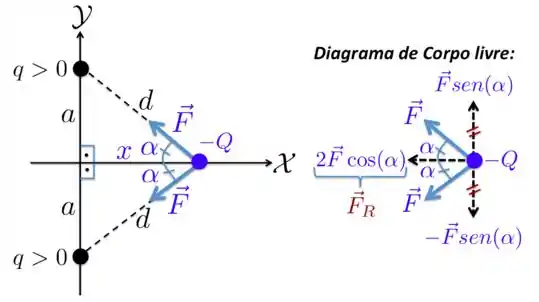
Fazer um diagrama de corpo livre aqui significa isolar a carga de interesse, no caso , e representar as forças que agem sobre ela, tipo o que mostramos na figura à direita acima!!! Como as forças são de atração e fazem um ângulo com o eixo , elas têm componentes tanto na direção , quanto na direção .
Passo 2
b) A gente vê que as componentes na direção se cancelam porque elas têm o mesmo módulo, a mesma direção, porém sentidos diferentes, por isso se cancelam. Então, na direção , o módulo força resultante é nulo:
Então, a gente só precisa mesmo olhar para as componentes sobre o eixo da força resultante. A soma das componentes em dará a força resultante . Essa força resultante será, então,
Sabemos que a intensidade da força entre e é dada pela lei de Coulomb, que é
Agora, dá uma olhada lá na figura para o triângulo retângulo. Olhou? Mesmo? Rsrs... Desse triângulo, podemos escrever que
Com as duas últimas expressões, conseguimos representar o móduloda força resultante como
e essa é a componente da força resultante: . Representando em termos de vetores
ou seja, a força resultante tem componente na direção , como mostramos para você lá na figura.
Passo 3
c) Para fechar o exercício, dá uma olhada na expressão para o vetor força resultante que acabamos de encontrar. Se você joga nessa expressão, obtém que
Sem fazer conta, para a gente checar se esse resultado tá ok ou não, imagina que a carga negativa está na origem. Nessa posição, as forças, devidas às cargas positivas , têm o mesmo módulo, mesma direção, porém sentidos contrários, já que as cargas estão à mesma distância da origem .
Isso significa que, em , realmente temos
Então fechou, a nossa conta tá correta...\0/
Resposta
- Diagrama de corpo livre representado na figura;