UFRJ – Física 3 2020.2 – P1 – Questão 36
Três partículas de cargas e estão localizadas nos pontos de coordenadas e , respectivamente. Sabendo que são os vetores unitários nas direções e , podemos dizer que a força resultante na partícula devido às outras duas partículas é dada por:
Escolha uma:
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas não é, saca só! Vou começar com um desenho da situação:
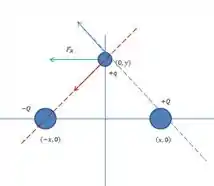
A carga que está em exerce uma força de repulsão na carga (em azul), enquanto que a outra carga, que está em , exerce uma força de atração (em vermelho). Então, pelo desenho podemos ver que a força resultante (em verde) será horizontal para a esquerda. Beleza?
Passo 2
E quanto ao módulo? Bom, a componente vertical é anulada, então precisamos encontrar apenas a componente horizontal.
Daí pelo desenho temos que:
A força é a força elétrica entre as cargas:
A distância entre elas é igual (para os dois pares) e temos:
E o ângulo com a horizontal:
Agora é só juntar tudo isso:
Na direção horizontal para a esquerda:
Beleza?
E analisando as alternativas, a correta é a (e).
Espero ter ajudado!