Dado um sistema isolado conforme discriminado abaixo:
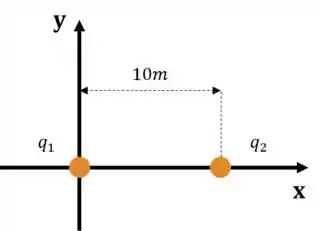
As cargas são dadas por: e .
Calcule o vetor força elétrica que a partícula 1 faz na 2 e o que a partícula 2 faz na 1.
Dado:
Passo 1
Aplicando a fórmula da força elétrica:
Substituindo os valores das cargas e da distância, podemos calcular o seu módulo:
Substituindo o valor de :
Passo 2
A partir daí, basta orientar a força de cada partícula. Como ambas tem a mesma carga, a força é repulsiva, ou seja, no sentido de afastar as duas.
Portanto, a carga vai fazer em uma força para a direita. Logo:
Ou, para quem gosta da outra notação, multiplicamos pelo vetor o módulo para que ele aponte na direção certa:
Passo 3
Pela mesma lógica, a partícula faz em uma força que aponta para a esquerda. Portanto:
Ou seja:
Sem fazer esse raciocínio, nós poderíamos também ter chegado à essa conclusão pela Lei de Newton da ação e reação.