Dada a configuração de cargas abaixo:
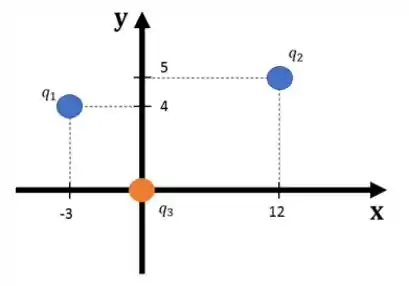
Onde:
Calcule a força resultante sobre a carga .
Passo 1
Para calcular a força resultante sobre a carga, basta somarmos todas as forças sendo exercidas nela, essa estratégia é conhecida também como superposição dos efeitos. Usaremos pra ambas as cargas a equação:
Onde é a direção da força entre a cargas e é o quadrado da distância entre elas. Vamos desenhar as distâncias das cargas até a carga
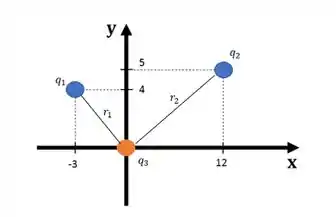
Então vamos começar calculando a força que faz em :
E encontramos a distância ao quadrado por Pitágoras:
Substituindo:
Passo 2
Agora precisamos achar o vetor unitário . É apenas um exercício de trigonometria. Sabemos que ele aponta de para :
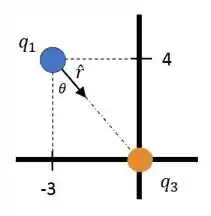
Decompondo, nós temos:
Agora temos:
Por consequência, obtemos:
Passo 3
Fazendo o mesmo processo para a interação entre as cargas 2 e 3:
Encontramos:
Portanto:
Passo 4
Buscamos agora encontrar o vetor que dá a direção da força que a carga 3 exerce em 2.
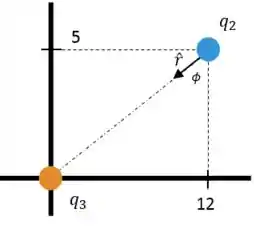
Temos:
Onde:
Portanto obtemos:
Passo 5
Para achar a força resultante, basta somar!
Não vamos nem brincar de arrumar isso aí, né? Ninguém merece.
O importante é você ter entendido a ideia.