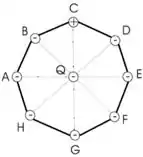
1ª questão - Em um octógono regular, cuja distância do centro a um dos vértices é , todos os vértices estão ocupados por cargas imóveis de mesmo módulo e com sinais indicados na figura. Qual é o módulo da força eletrostática sobre uma partícula (imóvel) de carga colocada no centro?
A)
B)
C)
D)
E)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão temos um octógono onde em cada vértice, a uma distância do centro, existe uma carga como descrito na imagem do enunciado e temos também uma carga negativa no centro do octógono.
Com essa distribuição de cargas temos que calcular a força eletrostática na carga central sendo que todas as cargas estão imóveis.
E aí, tem ideia de como podemos começar?? 🤔🤔
Pela Lei de Coulomb, o módulo da força eletrostática é dado pela formula
No caso, como temos mais de duas cargas, a força eletrostática é dada pelo somatório que cada uma das cargas contribui para nossa carga .
Entendeu? Vamos ver como é na prática! 😁😁
Passo 2
Sabemos que as cargas opostas se atraem e as cargas iguais se repelem. Vemos que a carga e a carga não negativas, portanto, se repelem. Da mesma forma a carga , , , , e .
A única exceção é a carga que é positiva, portanto, atrai a carga .
Dessa forma os vetores força eletrostática que agem em são
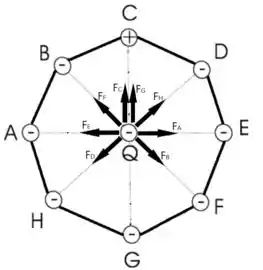
Foi dito no enunciado que todas as cargas de a são iguais em módulo, portanto, EM MÓDULO, todas as cargas vão exercer a mesma força.
Perceba então que algumas forças vão se anular, já que estão em sentidos opostos.
Consegue ver quais forças vão se cancelar? 🤔
Passo 3
Em outras palavras,
Portanto, e se cancelam, assim como e e também e .
Mas então podemos imaginar que tudo se cancela e a força resultante é igual a , não é? 👀
Porém, duas forças apontam para o mesmo sentido, no caso a força e .
A força eletrostática resultante não é o somatório das forças?
Se é dado por e a se é dado por , logo
Com isso, descobrimos que
A resposta correta para o nosso problema é a alternativa (C)!
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
C)