Considere um quadrado, com aresta de comprimento , com partículas em todos os seus 4 vértices, conforme mostra a figura.
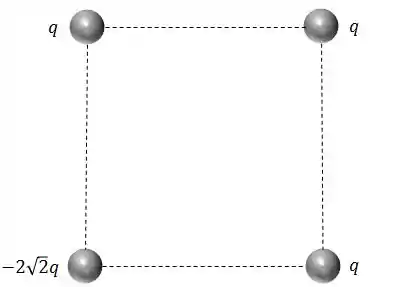
Qual é o módulo da força elétrica resultante sobre a partícula no vértice superior direito?
Passo 1
Beleza, vamos começar calculando o vetor força elétrica resultante sobre a partícula no vértice superior direito. Pra isso, vamos calcular, separadamente, as forças que cada outra partícula faz sobre a partícula que estamos interessados.
Lembrando que a força elétrica entre duas cargas é dada por:
Vamos começar numerando as cargas pra não nos enrolarmos:
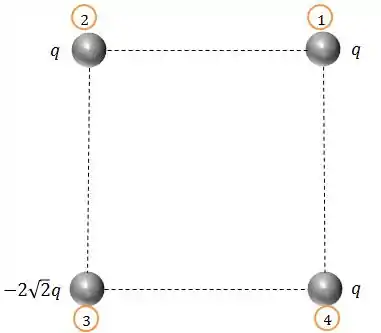
Levando em consideração os sinais das cargas, as forças terão os seguintes sentidos:
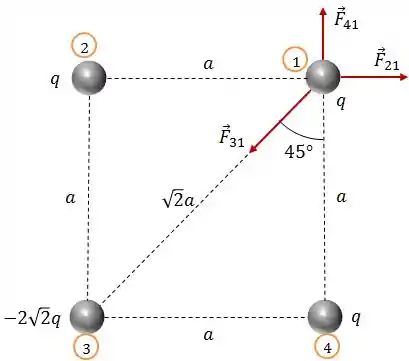
Agora já podemos começar a escrever as forças elétricas.
Passo 2
- Força elétrica de 2 sobre 1:
- Força elétrica de 4 sobre 1:
- Força elétrica de 3 sobre 1:
Finalmente, o vetor força resultante sobre a carga 1 será:
A resposta certa é a letra .
Resposta