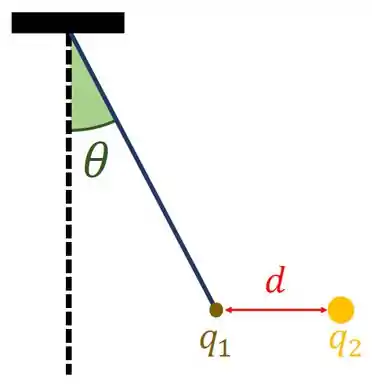
Na figura abaixo, uma pequena esfera de massa e carga é pendurada por um fio fino de massa desprezível. Uma segunda carga é mantida fixa a uma distância de , conforme a figura. Sabendo que é o módulo da aceleração da gravidade, quanto vale ?
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiramente, vamos relembrar a força de Coulomb.
Sejam duas cargas e Q separadas por uma distância . O módulo da força elétrica (ou de Coulomb) entre elas é dada pela seguinte expressão
com a constante eletrostática. A direção desta força é a direção de uma reta que vai do centro de uma carga até o centro da outra. O sentido da força depende do sinais das cargas em questão.
O enunciado diz que carga está pendurada por um fio fino de massa desprezível, tem massa e está sob influência de uma carga . Portanto, existem 3 forças que atuam sobre : a força peso, a força de tração devido ao fio e a força elétrica devido à carga , que é mantida fixa a uma distância de .
Assim, para determinar , podemos aplicar a 2ª lei de Newton na carga sabendo que ela se encontra em repouso. BORA LÁ!
Passo 2
Considere o diagrama de corpo livre da carga .
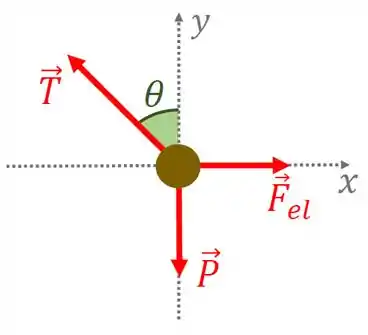
A força é a tração e se deve ao fio. A força é a força peso. Já a força é a força elétrica devido à carga .
Assim, como a carga está em repouso, temos que
Deste modo, agora basta tomar a razão entre as duas equações. Vamos lá
Assim, analisando todas as alternativas, vemos que a alternativa correta é a letra .