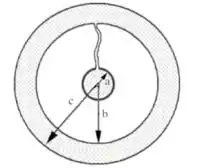
05) Uma esfera condutora maciça de raio '' possui carga . Concêntrica a ela, existe uma casca esférica espessa condutora e descarregada, de raio interno '' e raio externo '', onde . Em certo instante, conectamos a esfera e a casca esférica por um fio condutor, conforme ilustrado na figura. Quando as cargas atingem o equilíbrio:
a) A superfície interna da esfera oca tem carga e a esfera maciça tem carga .
b) A superfície externa da esfera oca tem carga e a esfera maciça tem carga .
c) A superfície interna da esfera oca tem carga e a esfera maciça tem carga .
d) A superfície externa da esfera oca tem carga e a esfera maciça tem carga .
e) A superfície externa da esfera oca tem carga e a esfera maciça tem carga .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Vamos imaginar a seguinte situação: temos uma esfera condutora que tem uma carga , essa esfera é concêntrica com uma casca esférica condutora que está envolta à esfera.
Essa casca esférica está descarregada e então decidimos ligar um fio entre ela e a esfera carregada.
Após um tempo, decidimos investigar qual é a distribuição de cargas no sistema.
Temos algumas opções e temos que assinalar qual é a opção que descreve essa situação nesse momento.
Entendeu? Como podemos fazer isso? 🤔
Que tal analisarmos cada alternativa separadamente e dizer o motivo de tal alternativa ser verdadeira ou falsa.
Bora lá? 😁
Passo 2
Antes, temos que compreender uma coisa!
Pela lei de Coulomb, as cargas elétricas tendem a se posicionar em um condutor de maneira que as forças de repulsão sejam as menores possíveis.
Lembrando que cargas de mesmo sinal se repulsam e de sinal contrário se atraem.
Agora sim...
A alternativa A) diz que a superfície interna da esfera oca tem carga e a esfera maciça tem carga .
Que tal? 🤔
Inicialmente a esfera interna está carregada com e a casca está descarregada, portanto não existem cargas , logo não é possível que essa situação aconteça.
Entendeu?

Bora pra próxima!
Passo 3
Na alternativa B) diz que a superfície externa da esfera oca tem carga e a esfera maciça tem carga .
Será mesmo? 👀
Se a esfera maciça tem carga inicialmente e a casca está descarregada, como é possível que em ambos tenham carga após a conexão? 🤔
Se analisarmos o a carga interna ao sistema para esse caso, vamos obter , o que não é possível.
Logo, a alternativa B) também está errada!

Entendeu?
Passo 4
Na alternativa C) diz que a superfície interna da esfera oca tem carga e a esfera maciça tem carga .
Será que agora vai? 👀
Como dizemos no passo 2, as cargas de mesmo sinal tendem a encontrar um lugar onde as forças que agem sobre elas são as menores possíveis.
A superfície da esfera é menor que as superfícies da casca, então o lugar onde as cargas vão sofrer menores forças é na casca, logo, as cargas tendem a se mover para ela.
Dessa forma, podemos afirmar que a alternativa C) também é falsa!

Bacana, não é? 😉
Passo 5
A alternativa D) diz que a superfície externa da esfera oca tem carga e a esfera maciça tem carga .
Agora será que vai? 😁
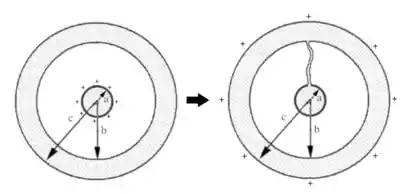
Seguindo o que falamos no item anterior, as cargas positivas da esfera tendem a encontrar um ponto onde as forças de repulsão entre elas sejam as menores possíveis.
Para isso elas devem estar com o maior afastamento entre elas, logo essa condição deve acontecer na maior superfície que elas podem encontrar, ou seja, na superfície externa à casca esférica.
Dessa forma, podemos afirmar que a alternativa correta é a letra D)!
Gostou? 😎
Passo 6
Por fim, vamos ver porque a alternativa E) é falsa.
Ela diz que a superfície externa da esfera oca tem carga e a esfera maciça tem carga .
Isso não pode ser verdade pois se fizermos o cálculo da carga interna do sistema, vamos obter .
Como inicialmente a carga do sistema é , não é possível que essa situação aconteça!
Entendeu? 😉
É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta
d) A superfície externa da esfera oca tem carga +Q e a esfera maciça tem carga 0.