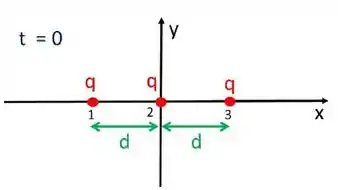
Três partículas idênticas, de massa e carga, se encontram no instante nas posições iniciais , ao longo do eixo , como mostra a Figura. Não considere nenhuma outra força, além das forças eletrostáticas, agindo sobre as partículas.
a) Calcule as forças resultantes sobre cada uma das partículas e, no instante inicial.
b) Calcule a energia eletrostática total no instante inicial.
Após o instante , as partículas são liberadas do repouso para se moverem livremente sob a ação das forças eletrostáticas.
c) Após um tempo muito longo, calcule as posições e velocidades de cada uma das três partículas acima.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
No instante inicial elas estão em repouso, então só temos as forças eletrostáticas envolvidas. A força resultante sobre a partícula é zero, por questão de simetria. Ela dista igual das duas outras cargas, então sobre ela a força resultante é zero.
Sobre a partícula temos duas forças: da carga a uma distância e da carga a uma distancia , a força resultante então será (na direção horizontal para a direita, já que as cargas são positivas):
E por simetria a força resultante na partícula será igual em módulo a da partícula , mas com sinal negativo, pois ela aponta na direção negativa de :
Passo 2
Letra (b):
A energia eletrostática também é calculada aos pares: , e . A energia vai com o inverso da distância. Então agora é só substituir:
Tranquilo? Vamos para o terceiro item?
Passo 3
Letra (c):
Aqui temos que a energia se conserva, então:
As partículas se afastam por completo, então ; No início as partículas estão em repouso, então . A partícula que está no meio fica em repouso, então na parte de energia cinética temos apenas as contribuições das partículas e , e elas contribuem igualmente, já que possuem a mesma massa. Assim a equação de conservação de energia fica:
A energia eletrostática inicial foi calculada no item anterior, então agora é só substituir:
Então as velocidades são:
Beleza?
Pronto pra próxima questão? =)