5ª questão - Um condutor neutro tem uma cavidade oca dentro dele. Dentro desta cavidade há uma carga de que não toca o condutor. Não há outras cargas nas proximidades. Qual afirmação sobre esse condutor é verdadeira?
A) A superfície interna do condutor carrega uma carga de e sua superfície externa não carrega carga em excesso.
B) A superfície interna e externa do condutor contêm cargas de .
C) O campo elétrico resultante dentro do material do condutor aponta para longe da carga de .
D) A superfície externa do condutor contém de carga e a superfície interna contém .
E) Ambas as superfícies do condutor não carregam excesso de carga porque o condutor está descarregado.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

O que temos para essa questão é um objeto condutor NEUTRO e oco. Dentro desse condutor, existe uma carga de que não encosta no condutor.
A partir daí, temos que analisar algumas afirmações e dizer qual é a verdadeira.
O que acha? Podemos fazer assim? 🤔
Antes de tudo, vamos pensar no nosso objeto. No enunciado foi dito que ele é um condutor neutro, ou seja, o número de elétrons é igual o numero de prótons e por ser condutor, significa que as cargas podem se movimentar livremente no objeto.
Entendeu? 😎
Passo 2
Para facilitar nosso entendimento, vamos imaginar que nosso objeto é uma casca esférica condutora e oca, como por exemplo
Vamos começar a analisar as afirmações? 👀
Na alternativa A) é dito que a superfície interna do condutor carrega uma carga de e sua superfície externa não carrega carga em excesso.
O que você acha? 🤔
Sabemos pela Lei de Coulomb que cargas de mesmo sinal se repelem e cargas de sinais opostos se atraem. Assim como temos uma casca esférica neutra que em seu interior existe uma carga positiva, certamente as cargas negativas da casca serão atraídas e as positivas serão repelidas.
Logo faz sentido que na superfície interna da casca, a carga seja de , mas se na superfície externa não houvesse excesso de cargas, a casca esférica não seria neutra, não é?
Então, por esse motivo, podemos afirmar que a alternativa A) é falsa!
Entendeu? 😁
Passo 3
Vamos analisar a alternativa B) que nos diz que a superfície interna e externa do condutor contêm cargas de .
Será mesmo?? 🤔
Com base no que dizemos no item anterior, as cargas opostas se atraem e as cargas de mesmo sinal se repelem. Então como é possível uma casca neutra ter uma carga de na superfície interna e externa ao mesmo tempo?
Pra isso acontecer, a casca esférica não poderia ser neutra, concorda?
Então a alternativa B) também é falsa!

Entendeu essa parte? 😉
Passo 4
Na alternativa C) diz que o campo elétrico resultante dentro do material do condutor aponta para longe da carga de .
Que tal? 😅
Essa alternativa diz a respeito de dentro do material da casca esférica, ou seja, não da parte oca, mas sim no espaço entre o raio interno e o raio externo.
A casca esférica é neutra, não é? Então lembra qual é o campo elétrico dentro de um condutor neutro? É , correto?
Dentro de qualquer condutor neutro, o campo elétrico é nulo, portanto, o campo não aponta para nenhum lado.
Logo, a afirmação C) também é falsa!

Tranquilo até aqui? 🤔
Passo 5
Na alternativa D) diz que a superfície externa do condutor contém de carga e a superfície interna contém .
Acha que agora vai? 😎
Partindo da ideia que debatemos nos itens anteriores, as cargas iguais se repelem e as cargas opostas se atraem. O que acontece é que como a casca esférica é eletricamente neutra (o número de elétrons é igual ao número de prótons) a carga interna de atrai as cargas negativas que estão na casca esférica e repele as cargas positivas da mesma.
Assim, as cargas negativas se aproximam do interior da casca, ou seja, na superfície interna pois são atraídas pela carga no interior da casca e as cargas positivas se aproximam da superfície externa pois são repelidas pela carga no interior da casca.
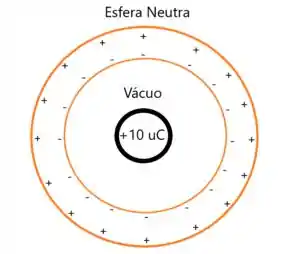
Com isso, vemos que a alternativa D) é verdadeira!
Interessante, não é? 😁
Passo 6
Por fim, vamos ver porque a alternativa E) é falsa.
Ela nos diz que ambas as superfícies do condutor não carregam excesso de carga porque o condutor está descarregado.
Hã?? 🤔🤔
A confusão que pode ocorrer nessa alternativa é que no enunciado diz que o condutor é neutro, mas isso não significa que ele está descarregado.
O condutor é neutro pelo motivo de o numero de cargas positivas ser igual ao numero de cargas negativas, ou seja, há carga no condutor, mas elas se neutralizam.
Diferentemente se o condutor estivesse descarregado, já que nesse formato, não haveria cargas nele.
Então é por isso que a alternativa E) é falsa!
Logo, a alternativa correta para o nosso problema é a alternativa D).
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta
D) A superfície externa do condutor contém de carga e a superfície interna contém .