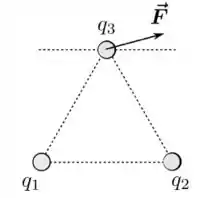
Três partículas carregadas, com cargas , e , são fixadas sobre os vértices de um triângulo equilátero, como mostrado na figura abaixo. Sabe-se que , enquanto e têm sinais e intensidades a serem determinadas. Para isso, mede-se a força eletrostática resultante que e exercem sobre e verifica-se que ela tem a direção e sentido mostrados na figura. Notando que a linha horizontal tracejada na figura é paralela ao lado horizontal do triângulo, podemos afirmar que:
a)
b)
c)
d)
e)
f)
g)
h)
Passo 1
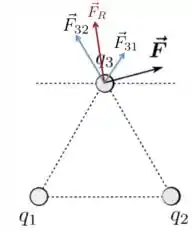
Vamos considerar primeiro a situação em que as duas cargas têm o mesmo sinal. Começando com o caso em que elas têm sinal positivo. Nesse caso, como mostra a Figura abaixo, teremos uma força resultante cujo vetor sobre a carga está entre os vetores e . Portanto, podemos excluir esse caso
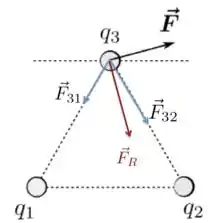
Se as duas cargas são negativas, o vetor resultante estará apontando para baixo, como na próxima Figura. Por isso, também podemos excluir esse caso de ambas as cargas serem negativas.
Portanto, as cargas precisam ter sinais opostos. Resta saber, agora, qual delas é positiva e qual é negativa.
Se e , então teremos uma força resultante em como na Figura abaixo.
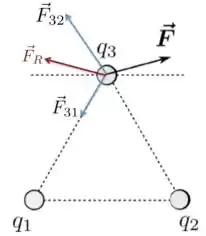
Dessa discussão, concluímos que devemos ter e . Falta sabermos como os módulos delas estão relacionados entre si.
Passo 2
Como já sabemos que e , então os vetores que temos são os da Figura abaixo.
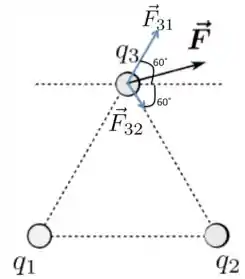
Dada essa Figura, podemos escrever os vetores e como
Portanto, somando vetorialmente as forças acima, a força resultante sobre a carga é
que é a expressão geral para a força resultante sobre a carga devida à sua interação com as cargas e .
Se os módulos das cargas fossem iguais, ou seja, , então, . Nesse caso, a força resultante sobre a carga se reduz a
ou seja, a força resultante estaria apontando na direção e sentido do vetor se .
Agora, da Figura que o problema dá, tem componente ao longo do eixo apontando para . Então, a partir da expressão geral para a força resultante que encontramos, temos que ter a seguinte condição
Passo 3
Colocando a expressão dada pela lei de Coulomb para o módulo da força na condição acima, teremos
de onde a gente tira que
Portanto, as cargas têm que ser tais que , e .
Resposta
Letra a).