Duas cargas puntiformes, cada uma com carga positiva , estão fixadas a uma distância entre elas. Considere uma terceira carga , também positiva, posicionada em uma altura genérica ao longo da bissetriz do eixo que separa as cargas (veja a figura abaixo) e inicialmente em repouso. A carga só pode se mover ao longo desta bissetriz.
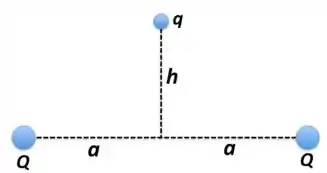
Escolha um sistema de coordenadas apropriado. Em seguida:
- Calcule a força elétrica (módulo, direção e sentido) exercida pelas duas cargas iguais a sobre a carga .
- Encontre a distância para a qual o módulo da força exercida sobre a carga é máximo.
- Calcule o módulo, direção e sentido da força elétrica no item b).
Considere, agora, que a carga da esquerda seja trocada por outra com o sinal negativo, .
d) Calcule, nesta nova condição, as respostas dos itens b) e c).
Passo 1
- Usando a coordenada cartesiana com eixo para cima, como mostra a figura abaixo, a força exercida é a soma dos componentes das forças exercidas por cada carga . As componentes horizontais se cancelam.
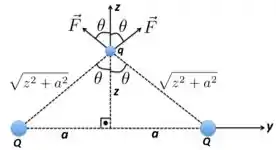
Então, a força na direção será dada por
sendo que, cada força individualmente é dada por
Lembrando que a distância entre e é , a hipotenusa dos triângulos retângulos da figura.
E o cosseno de sai da nossa figura! É isso aqui:
Juntando isso tudo, vamos ficar com
Botando a direção (que é pra cima!)
Passo 2
b) A força é máxima quando
Jogando a nossa força do passo anterior
Aí temos que fazer essa derivada chatinhaaaaa..... Pra isso temos que usar a regra do quociente (lembra dela?)
Onde e . As derivadas então serão
(Mole!)
(Não tão mole, mas fazer o que, né? ᷅\_(ヅ)_/ ᷄ ).
A nossa derivada vai ficar esse bicho feio aqui
Meio chatinho, mas dá pra simplificar um pouco colocando no numerador
Aí dá pra dar uma cortada em cima e em baixo e dá pra simplificar o que tá em colchetes!
Agora finalmente terminamos!
Agora temos que impor que essa expressão seja . Isso acontece quando o que tá nos colchetes for nulo, ou seja
Então, a força é máxima quando , tomando apenas a solução para , ou seja, considerando que está acima da linha que une as duas cargas .
Passo 3
A intensidade da força máxima aparece quando substituirmos na expressão pra força! Assim vamos ter
Simplificando:
Passo 4
d) Se trocamos a carga na esquerda com , teremos a situação ilustrada na figura abaixo. Nesse caso, a força tem componente horizontal no sentido da direita para a esquerda, ao longo da direção do eixo , e seu módulo será dado por: .
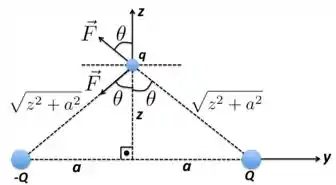
Nesse caso, como
teremos que o módulo da força resultante será:
Derivando com relação a e igualando a zero:
Substituindo na expressão para acima, teremos que a força máxima nesse caso será:
Resposta
- A força é máxima quando
- O valor da força máxima é
- A força será máxima quando
E seu valor será