(Cap 21 Ex – 22) A Fig. 21-30 mostra um sistema de quatro partículas carregadas,com e . A carga da partícula 2 é ; a carga das partículas e é . (a) Qual deve ser a distância entre a origem e a partícula para que a força que age sobre a partícula seja nula? (b) Se as partículas e são aproximadas do eixo mantendo-se simétricas em relação a esse eixo, o valor da distância é maior, menor ou igual ao do item (a)?
Passo 1
Falaii seres de luz, tudo belezinha?
Bora resolver essa comigo?
- Pra gente calcular a força total sobre a partícula , basta somarmos as forças ocasionadas pelas outras partículas sobre ela. Nós não sabemos se carga é positiva ou negativa, apenas sabemos que e são negativas, enquanto é positiva.
Logo, as forças feitas pelas cargas e são opostas ao efeito da carga . Supondo que a carga é positiva, temos as forças mostradas abaixo:
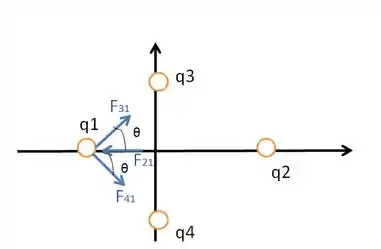
Lembrando que cargas de mesmo sinal se repelem e cargas de sinais diferentes se atraem!
Podemos decompor as forças no eixo e no eixo .
Vamos fazer isso olhando apenas para as componentes de força na direção nesse momento:
Lembrando que a força é dada pela equação:
Onde:
- é a constante eletrostática;
- é a carga da primeira carga;
- é a carga da segunda carga;
- é a distância entre as duas cargas.
Passo 2
Olha pra essas distâncias que eu separei pra você e vamos montar juntos as equações:
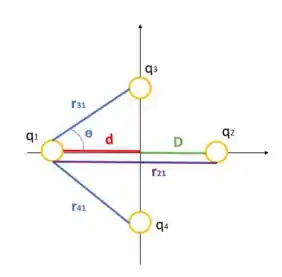
- A distância que vamos usar entre a carga 3 e a carga 1 é:
-
Logo a força que a carga 3 gera na carga 1 é igual a:
- A distância que vamos usar entre a carga 4 e a carga 1 é:
-
A mesma coisa que a carga 3, pois elas são simétricas em relação ao eixo . Logo a força que a carga 4 gera na carga 1 é igual a:
- A distância entre a carga 2 e a carga 1 é:
-
Logo a força será igual a:
Usando os valores das cargas em módulo:
Passo 3
Vamos colocar primeiramente os termos em evidência:
Se dividirmos os dois lados por esse termo em evidência:
Elevando os denominadores ao quadrado:
Passo 4
Simplificando as frações:
Vamos substituir os valores para continuar? O que ele nos deu no enunciado foi:
- e
Logo, vamos apenas utilizar o módulo das cargas:
Fazendo algumas contas:
Passo 3
Passando a expressão em função de para o numerador:
Vamos fazer a divisão do outro lado:
Temos uma função do segundo grau né, logo:
Como a distância deve ser positiva:
Chegamos em temos:
Passo 4
E chegamos em
Olhe bem para essa expressão. O que acontece se o ânculo diminuir?
Se ele diminui, 3 coisas acontecem:
- O valor de aumenta;
- Nisso, aumenta consequentemente;
Para compensar do outro lado o aumento do numerador do lado 1, devemos diminuir o denominador do lado 2.
Como não irá ser alterado, só podemos mudar . Logo precisamos diminuir esse !
Então, a gente pode afirmar com certeza que se as partículas e são aproximadas do eixo ( o que faz com que diminua), então a distância também deve diminuir.
Nesse caso, ela será menor que a do item a).
Resposta
- Menor