Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 21 – seção 4 - Problema 13.
(Cap 21 Ex – 13) Na Fig. 21-25, a partícula , de carga , e a partícula , de carga , são mantidas a uma distância uma da outra, em um eixo . Determine (a) a coordenada e (b) a coordenada de uma partícula de carga desconhecida para que a força total exercida sobre ela pelas partículas e seja nula.
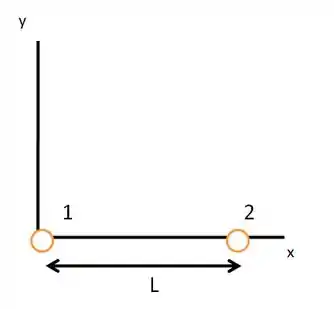
Passo 1
Faaaaaala galeinha bonitaa, animados?
A primeira coisa a fazer aqui é desenhar nossa carga três no sistema de coordenadas, ok?
Mas antes vamos pensar onde poderemos colocar esta carga!!
Se nós colocarmos a carga 3 entre as cargas 1 e 2 o que aconteerá ?
Como 1 e 2 tem cargas opostas, independente da carga de 3 uma delas vai atraí-la 3 para si e a outra repelir, o que nos gera duas forças na mesma direção !!
Então o meio não nos dá uma força resultante nulaa
E quando colocamos ela a direita de 2?
A carga de 2 é muito maior e possuirá uma distância muito menor do que a carga de 1 em relação a 3, a força que 2 exercerá será bem maior do que a de 1!!
Isso aí também vai gerar uma força resultante, não é?
Então a única opção que nos resta é coloca-la ela mais perto de 1, já que a carga dela é menor.
Vamos ver?
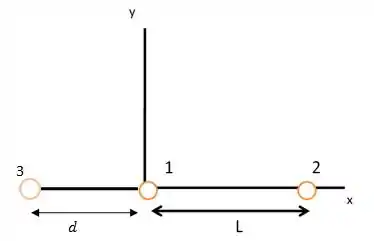
Sabemos que a força total exercida sobre ela pelas partículas e deve ser nula:
Até aqui tranquilnho, certo?
As forças elestrostáticas são dadas pela Lei de Coulomb:
Onde e são as cargas e a distância.
Colocando na igualdade:
Vamos tirar a raiz:
Lembrando que:
E substituindo:
Como d está 13,66 cm atrás da origem:
Passo 2
Bom, já achamos a letra (a), mas neste caso nós criamos uma suposição que o valo de y é zero, certo?
Mas porquê?
Como precisamos que as forças se anulem é preciso que uma seja oposta a outra, ou seja, paralelas entre si e com direções contrárias.
Isso só acontece quando a carga estiver localizadas no eixo .
Assim já respondemos a letra b, dizendo que a posição para que a força seja nula é:
Gostaram dessa?