Em um experimento, duas esferas de cobre idênticas, carregadas com a mesma carga , são mantidas próximas sem entrarem em contato uma com a outra. Uma das bolas é fixada no teto por meio de um bastão isolante. A outra bola é equilibrada em uma balança, cujo apoio é de plástico isolante. Nesta configuração, a balança registra gramas.
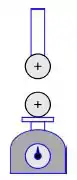
Na sequência, uma esfera idêntica descarregada toca na bola superior e é afastada. Após esse contato, a balança registra . Posteriormente, uma segunda esfera idêntica descarregada toca na bola superior e é afastada. Nesta situação, a balança registra .
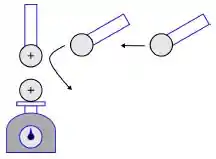
Quais das alternativas abaixo é correta?
Passo 1
Vamos analisar a força eletrostática entre a bola presa ao teto e a bola sobre a balança em cada uma das situações, certo?
Inicialmente, como as duas têm a mesma carga e estão sempre a uma distância fixa, que vamos chamar de , a força eletrostática entre elas será dada por:
Essa força corresponde à medição de gramas na balança.
Passo 2
Na segunda situação, após o contato da esfera descarregada com a esfera de cima, como ambas são iguais, atingido o equilíbrio eletrostático, as duas bolas terão uma mesma carga . Logo após o contato uma das bolas é afastada.
Assim, a força entre as esferas será dada por:
Essa força corresponde à medição de gramas. Comparando com o que encontramos no Passo 1, temos que:
Logo:
Passo 3
Por último, após o contato da esfera descarregada com a esfera de cima, atingido o equilíbrio eletrostático, as duas bolas terão uma mesma carga , sempre metade da carga anterior já que as bolas são iguais.
Dessa forma, a força de interação entre as bolas será:
Essa força corresponde à medição de gramas. Comparando com o que encontramos anteriormente, temos que:
Logo:
Finalmente:
![]()
Resposta