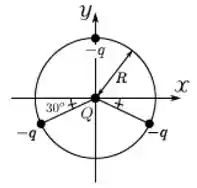
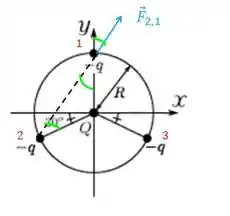
Três partículas de carga são posicionadas sobre um círculo de raio de forma que elas estão equidistantes uma da outra, como mostrado na figura abaixo. Uma quarta partícula de carga é posicionada sobre o centro deste círculo, que coincide com a origem do sistema de coordenadas indicado. Nessa situação, para que a força elétrica resultante sobre qualquer uma das partículas de carga seja nula, o valor de deve ser igual a:
a)
b)
c)
d)
e)
f)
g)
Passo 1
A primeira coisa de todas é lembrarmos qual a fórmula da força elétrica. Ela é dada por
Queremos encontrar qual o valor de tal que a soma de todas as forças nas cargas seja nula.
Como as cargas estão simetricamente espaçadas, a gente pode fazer a soma de forças em apenas uma delas e igualar a 0, e assim, encontramos a expressão para .
Passo 2
Vamos escolher a carga que está no eixo y, e fazer as contas com ela pra poder achar Q.
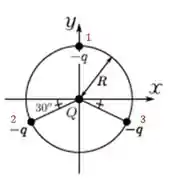
A força sobre essa carga 1 é:
A força é:
Sabemos que:
Mas qual a distancia r entre elas?
podemos descobrir por trigonometria, vamos fazer isso no próximo passo.
Passo 3
Vamos descobrir a distância formando o triângulo a seguir
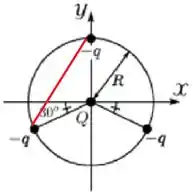
(Esse triângulo poderia ser entre quaisquer cargas -q, ia dar na mesma, ou seja a distancia r é a mesma entre 1 e2 e entre 1 e 3)
No caso, a gente tem um triângulo isósceles, pois dois lados dele são iguais (). O ângulo do meio, aquele que está ali no centro do círculo, vai ser , e como a soma dos ângulos internos de um triângulo deve ser , vamos ter o seguinte triângulo
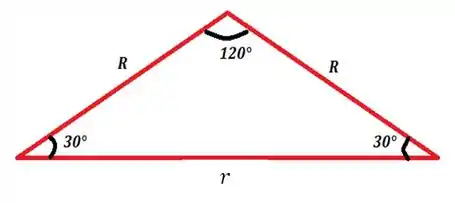
Agora é só a gente aplicar a lei dos senos pra descobrir :)
Booa! Agora que sabemos é só aplicarmos na fórmula da força elétrica lá do passo 2!
Passo 4
A força elétrica de 2 vai ser
Já temos todos os dados? Não! Mas tá quase. Só falta analisar a direção e sentido da força. Como ambas tem o mesmo sinal, a força vai ser repulsiva. Então vamos ter algo do tipo:
Já marquei ali os ângulos. Eles são iguais porque o triangulo é isósceles, de lado R. então o vetor força tem uma componente em y que é e uma componente em x que é . Agora sim! Vamos substituir isso tudo:
Beleza! Fazendo a mesma coisa para a força de 3 em 1, teremos algo do tipo:
Apareceu aquele menos ali no porque a força também é repulsiva, e está apontando no sentido negativo de x. Agora, vamos voltar lá naquela equação que vai dar todas as forças sobre a carga 1.
Substituindo o que já encontramos:
Arrumando isso:
Como o exercício pede que a força sobre qualquer carga –q seja nula, vamos igualar isso tudo a zero:
Então:
Então o módulo disso é:
Mas sabemos o módulo da força que Q faz em 1, pela equação do passo 1:
Certo?
Então, igualando as duas equações, temos:
Logo,
Show!!!
Resposta
A)