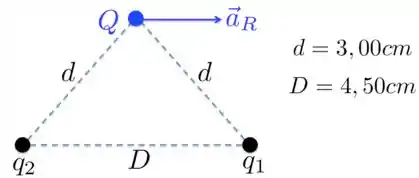
Duas cargas puntiformes e são mantidas fixas a uma distância de . Uma carga , de massa igual a , está inicialmente localizada a de cada uma dessas cargas, como mostra a figura abaixo e é libertada do repouso. Você verifica que a aceleração inicial de é da esquerda para a direita, paralela à linha que liga as duas cargas puntiformes. Dada essa situação, encontre os valores de e .

Neste exercício, a gente precisa descobrir primeiro para onde está apontando a força resultante  . A gente sabe que   está apontando na direção e sentido da aceleração  , pois, a partir da segunda Lei de Newton, temos o seguinte:

sendo a massa da partícula carregada negativamente . Isso está representado no figura abaixo. Aqui não vai entrar a força peso pois é como se as cargas estivessem todas no mesmo plano, então não vai ter ação da gravidade, beleza?

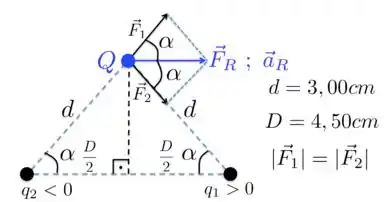
Também dessa figura, você consegue perceber que a carga deve ser negativa e a positiva, pois a soma vetorial tem que resultar em um vetor   apontando na direção e sentido da aceleração resultante  .

Além disso, como a força resultante   é paralela a linha que une as cargas e , o módulo das forças   e   devem ser iguais, ou seja, devemos ter que

que representamos na figura também. Isso também significa que temos também , tranquilo?? Ou seja, essas duas cargas tem sinais contrários e mesmo módulo!

Um aspecto que é importante você reparar é o seguinte: a força resultante que vamos considerar é a força inicial no instante inicial em que a carga é liberada, porque depois desse instante, a força muda de valor, já que a distância entre e as outras cargas vai mudar e, consequentemente, a aceleração também vai ser outra. Blz? Por isso o exercício tomou o cuidado de dizer aceleração inicial no ponto onde a carga negativa está.