Determine o volume máximo de uma caixa retangular cuja superfície tem e a soma dos comprimentos de todas as arestas é
Passo 1
Bora começar? Galera, é o seguinte. Primeiríssima coisa é dar nome aos bois. Temos uma caixa retangular, ou seja, um paralelepípedo. De forma genérica:
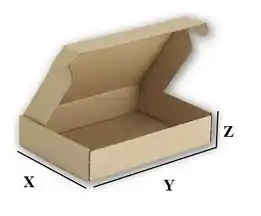
Onde, certamente:
Afinal, eu nunca vi uma caixa com tamanho negativo hahaha. A questão quer um volume máximo, então sabemos já que é uma questão de otimização multivariável. O volume vai ser definido por:
Mas calma lá galera, esse volume tem restrições. Afinal, a superfície () tem valor fixo de , isto é
E a soma dos comprimentos de todas as arestas também é fixa e dá , logo:
Já deu pra ver que vamos precisar usar Multiplicadores de Lagrange com duas Restrições. De e respectivamente, tiramos as seguintes restrições, ao dividir os dois lados por e , respectivamente:
Daqui em diante, o que faremos então será calcular:
O que é o mesmo que o sistema:
Mãos a obra!
Passo 2
Nesse passo vamos calcular as derivadas então, belê? A começar pelas derivadas parciais da fórmula do volume . Vamos ter:
Agora pra restrição , derivamos e achamos:
E por fim, pra restrição , derivamos e achamos:
O sistema de equações então se resume a:
Passo 3
Show galera, o que vamos fazer agora é mexer com as equações pra gerar as restrições necessárias. Veja que em todas elas a gente tem um solto que dá pra eliminar subtraindo uma equação da outra! Fazendo , achamos:
Colocando em evidência do lado esquerdo:
E colocando agora em evidência:
Portanto pra isso ser possível ou ou . Show! Mas isso aiiiinda não nos diz nada. Portanto, vamos precisar mexer mais com as equações do sisteminha. De forma parecida, bora fazer agora:
E colocando em evidência:
O que resulta em ou ou . Ai você vai me perguntar: tá, mas e dai? Veja bem, a gente sabe já que e satisfazem as equações, mas não sabemos quem é ! Relaxa que não tem problema, afinal se:
Então quem tá certo é a outra condição, pra cada um dos casos, que seria:
O que implica em ! Show! As condições que vamos testar então são:
Vamos usar cada uma dessas igualdades dentro da equação das restrições
E ver quais pontos surgem nesses casos. Partiu?
Passo 4
Primeiro caso:
Nesse caso, vamos ter nossas restrições se tornando:
O mesmo que:
Conseguimos isolar na segunda equação, achando . Usando essa equação dentro da primeira, achamos:
Opa, polinômio de segundo grau! Seja:
Calculamos:
Logo, o polinômio se reduz a:
Resultando em dois valores de possíveis:
Achamos o valor de bem rapidinho, nesse caso, se jogarmos dentro da restrição :
Resultando nos pontos:
Passo 5
Segundo caso:
É galera, não tem jeito, vamos repetir os procedimentos ok? Primeira coisa que fizemos antes foi reescrever as restrições, né não? A mesma coisa aqui! Elas vão virar
O que é o mesmo que:
E galera, olha só a macete! O nosso segundo caso ficou muito parecido com o primeiro! Só mudou quem chamamos de que! Se seguirmos a mesma estratégia e isolarmos , na primeira euqção vamos ter um polinômio de segundo grau de com a mesma cara do polinômio que achamos no passo anterior:
Resultando em dois valores de possíveis:
E pra esses valores, dentro da restrição , achamos os mesmos valores de :
Resultando nos pontos:
Terceiro caso:
Ok, vimos que o primeiro caso teve muita coisa em comum com o segundo, mas será que o terceiro tem também? Se você apostou que sim, apostou certo! Podemos até poupar contas (mas não poupa na prova não tá? Só aqui mesmo) e extrapolar. Como do caso pro acabou acontecendo isso:
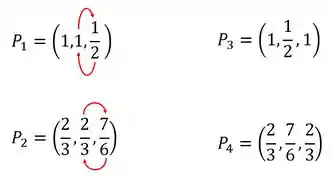
Do caso pro vai acabar acontecendo isso:
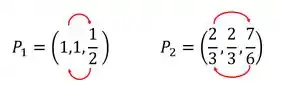
Gerando os últimos dois pontos:
Passo 6
Quase acabando galera! Conseguimos todos os pontos possíveis, mas como eles afetam o valor do volume!? Os pontos são:
E o volume é:
Pô pessoal, a função é um produto de todas as variáveis, então os pontos vão dar o mesmo resultado, já que eles são na prática só uma mudança de localização do . O volume, nesse caso, sera:
O mesmo vai valer pros pontos galera, pelo mesmíssimo motivo! Calculando o volume, achamos:
Então feshow galera! O volume máximo vai ser , já que esse valor é maior que .