Seja . Encontre os pontos de máximo e mínimo de no conjunto e .

Agora vamos definir:

Portanto, o conjunto é definido por:

e

Assim vamos poder ter restrições típicas de multiplicadores de Lagrange, do tipo e .

E para usar Lagrange vamos precisar dos gradientes das funções:

Show! Agora podemos procurar os candidatos a máximo e mínimo!

Vamos montar nossa estratégia para achar os máximos e mínimos de em todo o conjunto . Como vimos antes, temos e . Vamos subdividir essas duas inequações em 4 casos:

1. e
2. e
3. e
4. e

Assim estaremos cobrindo todo o conjunto !

Vamos ao caso 1:

e e

Só temos inequações então não vamos usar os multiplicadores de Lagrange, vamos apenas achar os pontos onde as derivadas parciais de dão , ou seja onde .

Lembrando que:

Logo:

A solução desse sistema vai ser:

Assim, achamos o ponto . E temos:

e

Portanto, o ponto pertence ao conjunto e é candidato a máximo ou mínimo.

Caso 2:

e e

Agora que temos a restrição podemos usar Lagrange, respeitando também a condição . Então partiu! Vamos ter:

Então nosso sistema vai ser:

A equação (1) nos dá mais 3 equações:

Assim, usando a segunda equação, a primeira fica:

Ou também podemos ter . Vamos analisar as opções:

• Se vamos ter: e . Nesse caso teríamos:

A equação do sistema não é respeitada.

• Se vamos ter: e . Mas devemos ter então essa opção também não é válida.
• Nos resta apenas a opção . Logo, pela equação :

Mas como :

Portanto, achamos o ponto candidato .

Caso 3:

e e

Vamos novamente aplicar Lagrange, com a restrição , o que nos dá:

E o nosso sistema vai ficar:

Essa vai ser fácil, já temos . Além disso, pela primeira equação:

Logo:

Podemos verificar que .

Achamos mais um candidato: o ponto . Agora vamos pro último caso!

Caso 4:

e e

Bem, agora temos duas restrições e . Então não tem jeito: vamos ter que usar 2 multiplicadores de Lagrange. Vamos ter que achar os pontos onde o gradiente da é uma combinação linear dos gradientes da e da . Ou seja:

Então vamos ter:

Sabemos que , então a segunda equação vai ficar assim:

Agora vamos dar uma olhada na primeira equação:

E:

Então caímos no sistema:

Opa! Já vimos isso antes, lá no caso 2 lembra? A gente concluiu que ou .

Show! Vai dar pra conciliar isso com a equação . Desse jeito:

Então vamos achar os candidatos e .

Depois desse trabalho todo, estamos chegando ao fim. Agora basta calcular o valor da em todos esses pontos que achamos e ver qual é o máximo e qual é o mínimo, demorô?

Lembrando que temos os pontos:

E também, pra refrescar a memória: .

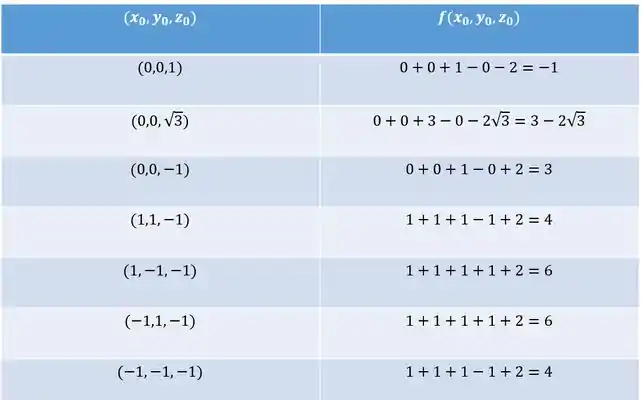
Note que é o maior valor: portanto os pontos de máximo de no conjunto são e .

Além disso, temos:

Portanto, o valor mínimo é e o ponto de mínimo de em é o ponto .