O plano corta o cilindro . Determine o ponto desta intersecção que está mais próximo e o que está mais distante da origem.
Passo 1
É o seguinte, a gente tem duas superfícies no espaço de tal modo que a intersecção delas forma uma curva:
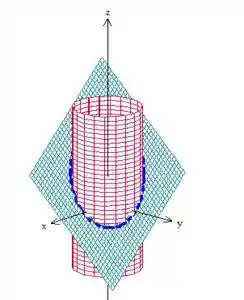
A gente quer encontrar os pontos dessa curva azul que estão mais afastados e mais próximos da origem. Como podemos encontrar isso?
Bem, trata-se de um problema de encontrar pontos máximos e mínimos da distância, certo? Então vamos usar o que a gente já sabe sobre a distância de um ponto no espaço até a origem:
Bem, mas qual é o detalhe aqui? Essa raiz horrível aí! Então vamos contornar esse problema pegando a função quadrado da distância:
Note que fazer isso não altera o problema, pois o maior (e o menor) valor dessa função, é também a da função distância , percebeu?
Passo 2
Para resolver o problema a gente vai utilizar os multiplicadores de Lagrange com duas restrições, se lembra?
EPA!!! A função até ok! É a função que queremos analisar, mas quem são essas outras duas aí?
Pow! Essas são as duas restrições do teorema. E elas são pra gente aqui, as equações que definem a curva!
Para a gente definir aquela e do problema, note que ambas estão igual a 1, logo, a gente pode considerar que essas superfícies são curvas de níveis 1 das funções
Passo 3
Para aplicar Lagrange, necessitamos das derivadas parciais de cada função definida, então vamos começar pela .
Fazendo o mesmo para a
E por último a de
Passo 4
Voltando para o teorema de Lagrange e substituindo esses caras
Multiplicando aquele lado de lá pelas constantes
Agora somando os vetores de lá
Dois vetores são iguais quando as mesmas posições são iguais, dessa forma
Não esqueça de adicionar as equações das superfícies aí, heim! Veja
Eita Geovana!!! Um sistema de 5 variáveis e 5 incógnitas, como sair disso? Me acompanha!:)
Passo 5
Primeiro, devemos ter claramente na ideia o que queremos para não nos perder. Queremos os valores , então vamos lá:
Note que a equação , pode ser substituída direta na equação
Se subtrairmos uma equação pela outra, teremos
Bem, aqui a gente se depara com duas situações possíveis para essa igualdade acontecer
- Se então não tem outro valor pra cá a não ser
- Ou e pode ser qualquer um nesse caso, pois
- Primeiro
- Segundo
- Terceiro
- Quarto
Passo 6
Vamos então analisar cada uma dessas condições separadas
Se a gente já sabe o termo só poderá ser nesse caso, como as únicas expressões que relacionam é a primeira ou a segunda, escolhemos uma delas
Substituindo o valo de
Quem é a única expressão que depende de ? Isso! A terceira
Substituindo agora esse resultado nas duas equações que a gente não trabalhou ainda e que tem
Substituindo então, obteremos...
Isolando o e jogando na de baixo
Simplificando...
Colocando em evidência
Assim, ou
ou
Como tivemos , já determinamos dois pontos aqui: e percebeu? Um ponto em e o outro, o outro
Passo 7
Mas ainda não terminamos, pois falta a outra condição do passo : se
Bem, aí podemos jogar essa expressão direto na expressão , logo substituindo...
Isolando o
Ok! Então se e ele é o negativo se for o negativo, entendi, mas e o ?
Bem, podemos tirar da única expressão que associa : , logo
Mas se
Logo, determinamos mais dois pontos aqui: e
Passo 8
Agora basta averiguar na função distância ao quadrado dos quatro pontos encontrados no total, , , e , é maior e menor
Elevando esses quadrados...
Podemos notar que o maior deles , logo é o ponto mais distante e os dois menores são e .
Como é menor que 3, então é maior que , por isso o ponto não entra na brincadeira, percebeu?