Seja . Obtenha os valores máximo e mínimo de no compacto e

Agora vamos calcular os gradientes de e de : se eles não forem paralelos, ou seja se o produto vetorial deles não der 0, então vamos poder aplicar a fórmula de Lagrange.

Esses gradientes são tranquilos de calcular para craques de derivação parcial como nós:

Agora poderíamos calcular o produto vetorial dos gradientes e verificar que não dá 0, mas uma outra boa forma de proceder é assumir que os gradientes são paralelos:

O que dá no sistema:

Agora que achamos uma relação entre , e , podemos jogar esses valores na expressão de ou . Como a função é mais simples, vamos usá-la:

E como vamos ter:

Vamos testar esses valores na equação da função e ver se verificamos ou não a nossa hipótese que os gradientes são paralelos:

Maaas, essa equação está claramente errada:

Atenção, estávamos apenas testando os valores, essas equações todas estavam erradas! Enfim, pelo menos podemos concluir que os gradientes de e não são paralelos e que o produto vetorial deles não dá :

Logo, se o ponto for um ponto de máximo ou mínimo local de , vamos ter, pelo método dos multiplicadores de Lagrange, que o gradiente de é uma combinação linear dos gradientes de e de .

Vamos dar uma olhada melhor nisso no próximo passo!

O nosso sistema de Lagrange fica assim:

Na verdade ainda nem calculamos o gradiente da , então vamos lá:

Olha como vai ficar o sistema:

A primeira equação desse sistema na verdade é composta de 3 equações. Então pra deixar como sendo só uma podemos usar o seguinte macete:

• Botar os gradientes de , e nas linhas de uma matriz 3x3
• Calcular o determinante da matriz
• Igualar o determinante a zero

Então vamos criar a matriz :

Já que vamos igualar o determinante a zero, podemos dividir as duas primeiras linhas por 2 pra simplificar. Podemos fazer isso porque multiplicando uma linha por um escalar multiplicamos também o determinante por esse escalar. E já que vai dar zero mesmo podemos multiplicar as linhas por o que queremos que não vai alterar o resultado. A matriz vai ficar assim:

Bem, agora é arregaçar as mangas e partir pras contas! Vamos aplicar a regra de Sarrus. A matriz expandida é:

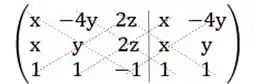
Na diagonal principal temos:

Diagonal secundária:

Logo:

Agora igualamos a zero e podemos aproveitar pra multiplicar por -1 para não lidar com sinais negativos:

Firmeza, agora nosso sistema ficou assim:

A partir da equação (1), vamos analisar as possíveis opções decorrentes, usando as outras equações do sistema, demorô?

ou

Opção 1:

A equação (2) nos dá:

E a equação (3):

Voltando pra (2):

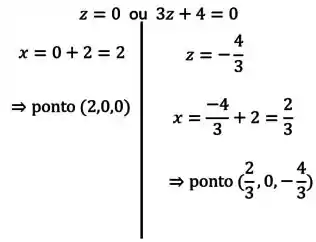
Opção 2:

Aplicando na equação (3):

Na equação (2) isso vai dar:

Portanto, achamos 4 pontos candidatos a máximo ou mínimo de no compacto :

Maas, infelizmente todas essas contas que fizemos foram sem considerar a inequação do enunciado (lembra?), ou seja até agora só consideramos a “borda” do compacto .

Já usamos a condição

Agora vamos ter:

Assim, juntando os dois casos, vamos ter respeitado a condição do enunciado:

Vamos manter a outra condição

Teremos que usar de novo Lagrange (pois é!) com a restrição ; mas só podemos selecionar os candidatos que respeitem a inequação aí de cima.

O gradiente da nós sabemos que é ; e o da é . O nosso sistema vai ficar assim:

Da equação (1) tiramos:

Aplicando isso na equação (3):

Opa! Achamos o ponto , que a gente viu logo antes!

Então essas contas não agregaram nada novo ao que a gente já sabia...mas elas eram necessárias.

Enfim, estamos quase acabando! Resta só determinar quais são os pontos de máximo e mínimo, dentre os nossos candidatos. Pra isso vamos calcular o valor da função em cada um desses pontos:

Portanto, o valor máximo de no compacto é , nos pontos e . O valor mínimo é , atingido no ponto .