Um cilindro de paredes adiabáticas é dividido em duas partições por um pistão móvel de área , também adiabático. As partições são preenchidas por moles do gás 1 e moles do gás 2, respectivamente. Ambos os gases são ideais e monoatômicos. A base do cilindro contendo o gás 1 é condutora térmica e encontra-se em contato com um reservatório térmico à temperatura , conforme indicado na figura abaixo. Inicialmente o pistão encontra-se em equilíbrio no centro do cilindro, dividindo-o em dois volumes iguais a :

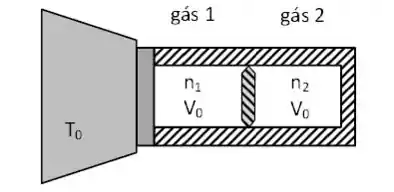
1. Determine a temperatura inicial do gás 1 e do gás 2.
2. Suponha agora que o pistão é deslocado lentamente por um agente externo até reduzir o volume do gás 2 à metade (). Qual a força exercida pelo agente externo na situação final deste processo?
3. Calcule o calor total recebido pelo gás 1 para o processo descrito no ítem (b).

b)

A força do agente externo tem que ser de tal forma que rquilibre a força que surgirá devido à diferença de pressão que aparecerá.

Afinal de contas, as pressões não serão mais iguais, já que um dos gases está sendo comprimido e o outro expandido.

Assim:

Assim, a força externa tem que ser igual a essa força para que se mantenha o equilíbrio:

Se o deslocamento foi feito lentamente, a temperatura continuou a mesma para o gás 1. Vale lembrar que existe uma transferência de calor do reservatório para o gás 1, nesse caso, já que a fronteira ali não é adiabática. Assim:

Então

O volume final é porque a compressão do gás 2 levou à uma expansão de para o gás 1.

Já o gás 2 sofreu uma compressão adiabática, já que a fronteira do gás 2 é adiabática. Assim, devemos usar a equação da transformação adiabática:

Lembrando que :

Show! Agora, substituindo na equação inicial:

c)

Como em 1 ocorre umas transformação isotérmica, temos:

Assim: