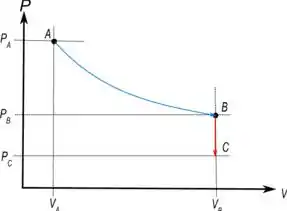
. Considere um gás ideal poliatômico em uma certa quantidade de tal forma que , onde é o número de mol. Inicialmente o gás se encontra a uma pressão e um volume e logo em seguida é realizado um processo adiabático (no gráfico representado pela curva contínua em azul) até o ponto com pressão e volume . Depois é realizado um segundo processo a volume constante (no gráfico representado pela seta contínua em vermelho) até o ponto que possuí uma pressão . A troca de calor no processo a volume constante é (o sinal indica perda de calor).
Qual a temperatura do ponto , ?
Dados:
.
.
.
.
.
. Nenhuma das alternativas
.
.
Passo 1
Vem comigo que juntos resolvemos essa questão!
Vamos analisar o processo a volume constante, nesse tipo de processo o trabalho realizado é zero, então a primeira lei da termodinâmica, fica de seguinte maneira:
O calor perdido nesse processo foi dado pelo enunciado e a variação de energia interna de um gás ideal poliatômico é dada por:
Onde .
Então temos que saber a temperatura para podermos achar . Para fazer isso vamos podemos usar a equação dos gases ideais para o ponto , temos:
Mas ainda temos um problema, não sabemos o valor de , mas calma, o processo de para é um processo adiabático e nesse tipo de processo temos o seguinte:
Então temos que:
Então podemos calcular o valor de dessa equação já que o enunciado dá todos os outros parâmetros e que para um gás poliatômico.
Mãos à obra então!
Passo 2
Vamos primeiro achar o volume , temos:
Substituindo os valores que temos, ficamos com:
Com isso temos que:
Passo 3
Agora que temos o valor de podemos encontrar , temos:
Usando que , segundo o enunciado, temos:
Passo 4
Agora podemos encontrar , temos:
Usando os valores que conhecemos, ficamos com:
Com isso vemos que a alternativa mais próxima é a letra .