UTFPR– Física 1 – Provas - Teste 9 – AV2 – 2022.2 – questão 5c
Ao ser posicionada a uma distância de do centro de um prato giratório, o qual realiza duas voltas em , uma bolinha de não escorrega. Determine (c) o módulo e a orientação da força centrípeta que atua sobre a bolinha.
Obs.: todas as respostas devem estar em unidades do SI.
Dica da prof.: para determinar a orientação tanto da aceleração centrípeta quanto da força centrípeta, basta dizer se são radiais para dentro ou para fora da circunferência.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinar qual é o módulo e a orientação da força centrípeta da bolinha que dá duas voltas em um prato giratório de tal forma que ela se localiza a do centro
Obs: a bolinha leva para realizar essas duas voltas.
Lembrando que a força centrípeta é dada por:
Onde é a massa da bolinha e é a sua aceleração centrípeta.
Agora bora resolver!!
Passo 2
Bom... pela questão anterior, descobrimos que a bolinha tem aceleração centrípeta igual a .
Dessa forma, podemos descobrir o módulo da aceleração centrípeta:
Passo 3
A orientação da força centrípeta é a mesma da aceleração centrípeta.
Dessa forma, por definição, a aceleração centrípeta possui direção radial no sentido para dentro da circunferência.
Se liga na imagem abaixo:
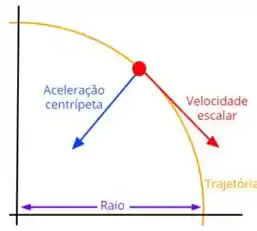
Entendeu direitinho? Responde aee ;)
Resposta
Para dentro da circunferência