[ENUNCIADO COMUM ÀS QUESTÕES 1 e 2]
Dois carros (A e B) movem-se em pistas paralelas e têm gráficos de posição em função do tempo mostrados na Figura.
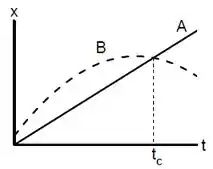
[QUESTÃO 2]
As equações horárias dos carros são e respectivamente, onde é medido em segundos e em metros. Determine em que instante os carros têm a mesma velocidade instantânea.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i) Nunca
Passo 1
A velocidade é a variação da posição, ou seja, sua derivada:
Então, basta nós derivarmos as expressões de posição para achar as expressões das velocidades instantâneas de ambos.
Passo 2
Derivando :
Passo 3
Derivando :
Passo 4
Para saber o instante em que as velocidades se igualam, basta igualar as expressões:
No instante as velocidades são as mesmas.
Resposta
Letra (d)
Exercícios de Livros Relacionados
Duas partículas se movem ao longo do eixox . A posição da partícula 1 é dada por x = 6,00 t 2 +3,00 t + 2,00 , onde x está em metros e t em segundos; a aceleração da partícula 2 é dada por a =- 8,00 t
A função posição x ( t ) de uma partícula que está se movendo ao longo do eixo x é x = 4,0 -6,0 t 2 , com x em metros e t em segundos. (a) Em que instante e (b) em que posição a partícula para (moment
Com base em sua experiência de dirigir um automóvel, estime o módulo da aceleração média de um carro quando a) acelera em uma estrada do repouso até 65 mi/h e b) pisa forte no freio até uma parada rep
2.13 O carro mais rápido (e mais caro)! A tabela mostra dados de teste para o Bugatti Veyron, o carro mais veloz já fabricado. O carro se move em linha reta (eixo 0x).a) Desenhe um gráfico v x t da ve
A aceleração de uma motocicleta é dada pora x t = A t - B t 2 , onde A = 1,5m / s 3 e B = 0,120m / s 4 . A motocicleta está em repouso na origem no instante t = 0 . a) Calcule sua velocidade e posição